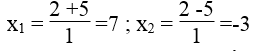✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

12/07/2024 2,058

Chứng minh rằng khi a và c trái dấu thì phương trình trùng phương a $x^{4}$ +b $x^{2}$ +c =0 chỉ có hai nghiệm và chúng là hai số đối nhau

Xem lời giải

Câu hỏi trong đề: Giải Sách Bài Tập Toán 9 Tập 2 !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đặt m = $x^{2}$ .Điều kiện m $\geq$ 0

Ta có: a $x^{4}$ +b $x^{2}$ +c = 0 ⇔ a $m^{2}$ + bm + c = 0

Vì a và c trái dấu nên a/c < 0. Phương trình có 2 nghiệm phân biệt là $m_{1}$ và $m_{2}$

Theo hệ thức Vi-ét,ta có: $m_{1}$ $m_{2}$ = c/a

Vì a và c trái dấu nên c/a <0 suy ra $m_{1}$ $m_{2}$ < 0 hay $m_{1}$ và $m_{2}$ trái dấu nhau

Vì $m_{1}$ và $m_{2}$ trái dấu nhau nên có 1 nghiệm bị loại ,giả sử loại $m_{1}$

Khi đó $x^{2}$ = $m_{2}$ => x = $\pm$ $\sqrt{m_{2}}$

Vậy phương trình trùng phương a $x^{4}$ +b $x^{2}$ +c = 0 chỉ có hai nghiệm và chúng là hai số đối nhau khi a và c trái dấu

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Giải các phương trình trùng phương $x^{4}$ -8 $x^{2}$ – 9 =0

Xem đáp án

Lời giải

Đặt m = $x^{2}$ .Điều kiện m $\geq$ 0

Ta có: $x^{4}$ -8 $x^{2}$ – 9 =0 ⇔ $m^{2}$ -8m -9 =0

Phương trình $m^{2}$ - 8m - 9 = 0 có hệ số a = 1,b = -8,c = -9 nên có dạng a – b + c = 0

suy ra: $m_{1}$ = -1 (loại) , $m_{2}$ = -(-9)/1 =9

Ta có: $x^{2}$ =9 ⇒ x= $\pm$ 3

Vậy phương trình đã cho có 2 nghiệm : $x_{1}$ =3 ; $x_{2}$ =-3

Câu 2

Giải các phương trình: $\frac{12}{x - 1} - \frac{8}{x + 1} = 1$

Xem đáp án

Lời giải

Điều kiện : x $\neq \pm$ 1

Ta có: $\frac{12}{x - 1} - \frac{8}{x + 1} = 1$ ⇔ 12(x +1) – 8(x -1) = (x +1)(x -1)

⇔ 12x +12 -8x +8 = $x^{2}$ -1 ⇔ $x^{2}$ -4x -21 =0

$∆$ ’ = ${(- 2)}^{2}$ -1.(-21) = 4 + 21=25 > 0

$\sqrt{∆'} = \sqrt{25}$ =5

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Giá trị của x thỏa mãn điều kiện bài toán

Vậy nghiệm của phương trình là x =7 và x =-3

Câu 3

Giải các phương trình: $\frac{x^{2} - 3 x + 5}{(x - 3) (x + 2)} = \frac{1}{x - 3}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Giải các phương trình: $x^{4}$ - 2 $x^{3}$ + 3 $x^{2}$ - 2x + 3 = 0

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Giải các phương trình: $\frac{16}{x - 3} + \frac{30}{1 - x} = 3$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Giải các phương trình sau bằng cách đưa về phương trình tích ${(2 x^{2} + 3)}^{2}$ -10 $x^{3}$ -15x =0

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Giải các phương trình sau bằng cách đưa về phương trình tích 3 $x^{3}$ +6 $x^{2}$ -4x =0

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Vietjack official store

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

🔥 Đề thi HOT:

Bạn vui lòng để lại thông tin để được
TƯ VẤN THÊM

Hoặc gọi Hotline tư vấn: 084 283 45 85
Email: vietjackteam@gmail.com

VietJack