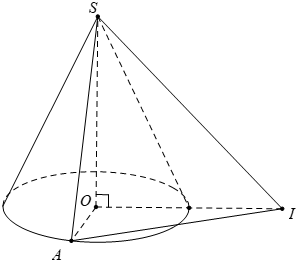
Một hình nón có đường kính đáy là 2a3, góc ở đỉnh là 120°. Tính thể tích của khối nón đó theo a. A. 3πa3 B. πa3 C. 23πa3 D. 3πa3

Câu hỏi:

20/02/2021 1,882

Một hình nón có đường kính đáy là 2a $\sqrt{3}$ , góc ở đỉnh là 120°. Tính thể tích của khối nón đó theo a.

A. $3 {πa}^{3}$

B. ${πa}^{3}$

C. $2 \sqrt{3} {πa}^{3}$

D. $\sqrt{3} {πa}^{3}$

Xem lời giải

Câu hỏi trong đề: 20 câu trắc nghiệm: Ôn tập chương 2 Hình học 12 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án B

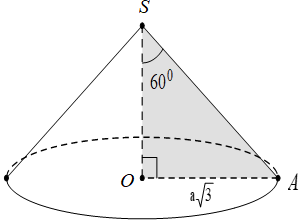
Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.

Theo giả thiết dễ suy ra đường tròn đáy có bán kính

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình nón đỉnh S với đáy là đường tròn tâm O bán kính R. Gọi I là một điểm nằm trên mặt phẳng đáy sao cho OI = R $\sqrt{3}$ . Giả sử A là điểm nằm trên đường tròn (O; R) sao cho OA ⊥ OI. Biết rằng tam giác SAI vuông cân tại S. Khi đó, diện tích xung quanh $S_{xq}$ của hình nón và thể tích V của khối nón là:

A. $S_{xq} = {πR}^{2} \sqrt{2}; V = \frac{{πR}^{3}}{3}$

B. $S_{xq} = 2 {πR}^{2}; V = \frac{2 {πR}^{3}}{3}$

C. $S_{xq} = \frac{{πR}^{2} \sqrt{2}}{2}; V = \frac{{πR}^{3}}{6}$

D. $S_{xq} = {πR}^{2}; V = \frac{2 {πR}^{3}}{3}$

Lời giải

Đáp án A

Câu 2

Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng a $\sqrt{2}$ và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Diện tích xung quanh $S_{xq}$ của hình nón và thể tích V của khối nón tương ứng là:

A. $S_{xq} = {πa}^{2}; V = \frac{{πa}^{3} \sqrt{6}}{12}$

B. $S_{xq} = \frac{{πa}^{2}}{2}; V = \frac{{πa}^{3} \sqrt{3}}{12}$

C. $S_{xq} = {πa}^{2} \sqrt{2}; V = \frac{{πa}^{3} \sqrt{6}}{4}$

D. $S_{xq} = {πa}^{2}; V = \frac{{πa}^{3} \sqrt{6}}{4}$

Lời giải

Đáp án A

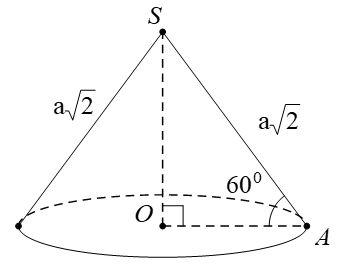
Gọi A là một điểm thuộc đường tròn đáy hình nón. Theo giải thiết ta có đường sinh SA = a $\sqrt{2}$ và góc giữa đường sinh và mặt phẳng đáy là $\hat{SAO}$ = 60°.

Câu 3

Cho hình nón tròn xoay có đường cao 12cm và đường kính đáy 10cm. Độ dài đường sinh của hình nón là:

A. $\sqrt{119}$ (cm)

B. 17 (cm)

C. 15 (cm)

D. 13 (cm)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình vuông cạnh a và cạnh bên bằng 2a. Thể tích khối nón có đỉnh là tâm O của hình vuông A'B'C'D' và đáy là hình tròn ngoại tiếp hình vuông ABCD là:

A. $\frac{{πa}^{3}}{3}$

B. ${πa}^{3}$

C. $\frac{2 {πa}^{3}}{3}$

D. $\frac{2 {πa}^{3} \sqrt{2}}{3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình chóp tứ giác đều S.ABCD có AB = a và góc giữa SA và đáy là 60^o. Bán kính mặt cầu tâm A tiếp xúc với mặt phẳng (SBC) là:

A. $\frac{a \sqrt{42}}{6}$

B. $\frac{a \sqrt{42}}{14}$

C. $\frac{a \sqrt{42}}{7}$

D. $\frac{2 a \sqrt{42}}{7}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình chóp tam giác đều S.ABC, mặt phẳng (SBC) tạo với đáy một góc bằng 30^o và SA = 2a. Thể tích khối cầu ngoại tiếp hình chóp S.ABC là:

A. $\frac{52 {πa}^{3} \sqrt{13}}{3}$

B. $\frac{4 {πa}^{3}}{3}$

C. $72 {πa}^{3} \sqrt{2}$

D. Đáp án khác

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Một hình nón có đường kính đáy là 2a $\sqrt{3}$ , góc ở đỉnh là 120°. Tính thể tích của khối nón đó theo a.

Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng a $\sqrt{2}$ và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Diện tích xung quanh $S_{xq}$ của hình nón và thể tích V của khối nón tương ứng là:

Cho hình chóp tứ giác đều S.ABCD có AB = a và góc giữa SA và đáy là 60^o. Bán kính mặt cầu tâm A tiếp xúc với mặt phẳng (SBC) là:

Cho hình chóp tam giác đều S.ABC, mặt phẳng (SBC) tạo với đáy một góc bằng 30^o và SA = 2a. Thể tích khối cầu ngoại tiếp hình chóp S.ABC là: