Quảng cáo
Trả lời:
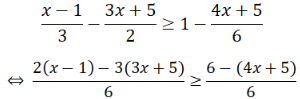
⇔ 2x - 2 - 9x - 15 ≥ 6 - 4x - 5
⇔ 2x - 9x + 4x ≥ 6 - 5 + 2 + 15
⇔ -3x ≥ 18
⇔ x ≤ -6
Vậy tập nghiệm của phương trình là S= {x|x ≤ -6}
Biểu diễn nghiệm trên trục số:
![]()
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) 8( 3x - 2 ) - 14x = 2( 4 – 7x ) + 15x
⇔ 24x – 16 -14x = 8 – 14x + 15x
⇔ 10x -16 = 8 + x
⇔ 9x = 24
⇔ x = 24/9
b) ( 3x – 1 )( x – 3 ) – 9 + x2 = 0
⇔ (3x -1)( x – 3) + (x - 3)( x + 3) = 0
⇔ (x - 3)(3x - 1 + x - 3) = 0
⇔ (x - 3)(4x - 4) = 0
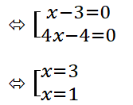
c) |x - 2| = 2x - 3
TH1: x - 2 ≥ 0 ⇔ x ≥ 2
Khi đó: x - 2 = 2x – 3
⇔ 2x – x = -2 + 3
⇔ x = 1 (không TM điều kiện x ≥ 2)
TH2: x – 2 < 0 ⇔ x < 2
Khi đó: x-2 = -(2x – 3)
⇔ x – 2 = -2x + 3
⇔ 3x = 5
⇔ x = 5/3 ( TM điều kiện x < 2)
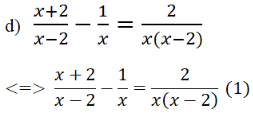
MTC: x(x-2)
ĐKXĐ: x ≠ 0;x ≠ 2
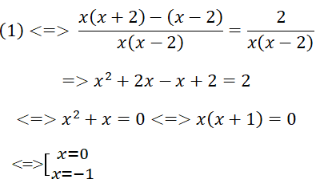
Đối chiếu với ĐKXĐ thì pt có nghiệm x = - 1
Lời giải
A = -x2 + 2x + 9 = -(x2 – 2x + 1) + 10 = - (x + 1)2 + 10
Ta có: - (x + 1)2 ≤ 0 ∀x
- (x + 1)2 + 10 ≤ 10
Dấu bằng xảy ra khi (x + 1)2 = 0 ⇔ x = -1
Vậy GTLN của A là 10, đạt được khi x = -1
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.