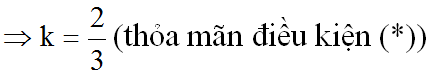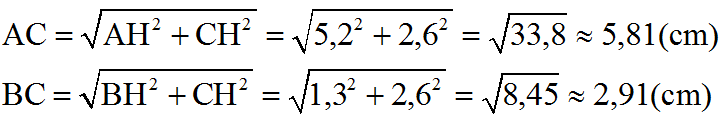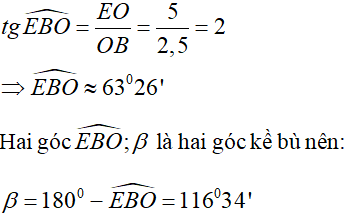Câu hỏi:
13/07/2024 18,495Khi nào thì hai đường thẳng y = ax + b ( a ≠ 0) và y = a'x + b' (a' ≠ 0) cắt nhau? Song song với nhau? Trùng nhau?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hai đường thẳng y = ax + b và y = a'x + b' (a, a' ≠ 0)
- Cắt nhau khi và chỉ khi a ≠ a'
- Song song với nhau khi và chỉ khi a = a', b ≠ b'
- Trùng nhau khi và chỉ khi a = a', b = b'
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hàm số y = ( k + 1)x + 3 có các hệ số a = k + 1, b = 3
Hàm số y = (3 – 2k)x + 1 có các hệ số a' = 3 - 2k, b' = 1
Hai hàm số là hàm số bậc nhất nên a và a' khác 0, tức là:
a) Theo đề bài ta có b ≠ b' (vì 3 ≠ 1)
Nên hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 song song với nhau khi a = a'
tức là: k + 1 = 3 – 2k
b) Hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 là hàm số bậc nhất nên a ≠ 0 và a' ≠ 0. Hai đường thẳng này cắt nhau khi a ≠ a' tức là:
Vậy với 
thì đồ thị của hai hàm số trên là hai đường thẳng cắt nhau.
c) Do b ≠ b' (vì 3 ≠ 1) nên hai đường thẳng không thể trùng nhau với mọi giá trị k.
Lời giải
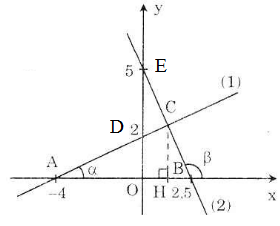
a) - Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0 => y = 2 được D(0; 2)
Cho y = 0 => 0 = 0,5.x + 2 => x = -4 được A(-4; 0)
Nối A, D ta được đồ thị của (1).
- Vẽ đồ thị hàm số y = 5 – 2x (2)
Cho x = 0 => y = 5 được E(0; 5)
Cho y = 0 =>0 = 5 – 2x => x = 2,5 được B(2,5; 0)
Nối B, E ta được đồ thị của (2).
b) Ở câu a) ta tính được tọa độ của hai điểm A và B là A(-4 ; 0) và B (2,5 ; 0)
Hoành độ giao điểm C của hai đồ thị (1) và (2) là nghiệm của phương trình:
0,5 x + 2 = 5 - 2x
⇔ 0,5x + 2x = 5 – 2
⇔ 2,5.x = 3 ⇔ x = 1,2
⇒ y = 0,5.1,2 + 2 = 2, 6
Vậy tọa độ điểm C(1,2; 2,6).
c) AB = AO + OB = |-4| + |2,5| = 6,5 (cm)
Gọi H là hình chiếu của C trên Ox, ta có H( 1,2; 0)
Ta có: AH = AO + OH = 4 + 1,2 = 5,2
BH = BO – OH = 2,5 – 1,2 = 1,3
CH = 2,6
d) Gọi α là góc hợp bởi đường thẳng y = 0,5x + 2 với tia Ox.
Ta có: tgα = 0,5 => α = 26o34'
Gọi β là góc hợp bởi đường thẳng y = 5 - 2x với tia Ox
Tam giác OEB vuông tại O nên:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận