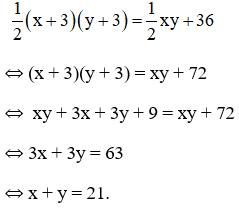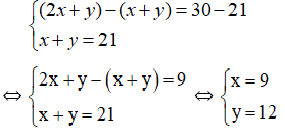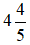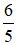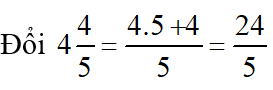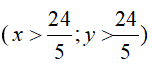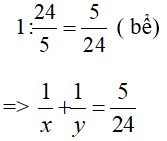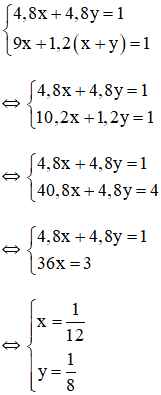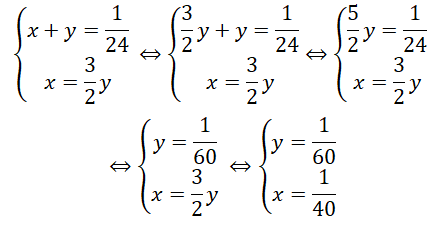Tính độ dài hai cạnh góc vuông của một tam giác vuông, biết rằng nếu tăng mỗi cạnh lên 3cm thì diện tích tam giác đó sẽ tăng thêm 36 , và nếu một cạnh giảm đi 2cm, cạnh kia giảm 4cm thì diện tích của tam giác giảm đi 26 cm2.
Quảng cáo
Trả lời:
Gọi x (cm) , y (cm) là độ dài hai cạnh góc vuông của tam giác vuông (x > 2, y > 4).
Diện tích tam giác ban đầu là (cm2)
+ Tăng mỗi cạnh lên 3cm thì tam giác vuông mới có độ dài 2 cạnh là x + 3(cm) và y + 3 (cm)
Diện tích tam giác mới là: (cm2)
Diện tích tăng thêm 36cm2 nên ta có phương trình:
+ Giảm một cạnh 2cm và giảm cạnh kia 4cm thì tam giác vuông mới có 2 cạnh là : x – 2 (cm) và y – 4 (cm).
Diện tích tam giác mới là: (cm2).
Diện tích giảm đi 26cm2 nên ta có phương trình
Lấy phương trình thứ hai trừ phương trình thứ nhất ta được:
Vậy tam giác có hai cạnh lần lượt là 9cm và 12cm.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Cách 1.
Gọi thời gian để vòi thứ nhất, vòi thứ 2 chảy 1 mình đầy bể là x (h), y (h).
+ Một giờ vòi thứ nhất chảy được :1/x ( bể )
Một giờ vòi thứ hai chảy được :1/y ( bể )
+ Hai vòi nước cùng chảy vào một bể nước cạn (không có nước) thì sau giờ đầy bể.
=> Một giờ cả hai vòi chảy được :
* Nếu ban đầu mở vòi 1 và 9 giờ sau mở thêm vòi 2 thì sau 6/5 (h) đầy bể. Khi đó, thời gian vòi 1 chảy là : .
Thời gian vòi 2 chảy là 6/5 (h)
Vậy nếu ngay từ đầu chỉ mở vòi 2 thì sau 8 giờ sẽ đầy bể.
Cách 2.
Gọi lượng nước vòi thứ nhất và vòi thứ hai chảy một mình trong 1 giờ lần lượt là x (bể) và y (bể).
Điều kiện 0 < x, y < 1.
+ Cả hai vòi cùng chảy trong 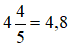
+ Nếu mở vòi thứ nhất trong 9 giờ thì chảy được 9x (bể)
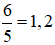
Khi đó bể đầy nên ta có phương trình: 9x + 1,2(x + y) = 1.
Ta có hệ phương trình
⇒ một giờ vòi hai chảy một mình được 1/8 bể
Vậy nếu ngay từ đầu chỉ mở vòi thứ hai thì sau 8 giờ sẽ đầy bể.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
Lời giải
Gọi x là số phần công việc làm trong 1 ngày của đội A
y là số phần công việc làm trong 1 ngày của đội B
Một ngày cả hai đội làm được 1/(24 ) công việc nên ta có phương trình:
x + y = 1/24
Mỗi ngày phần việc của đội A gấp rưỡi đội B nên ta có phương trình
x = 3/2 y
Do đó, ta có hệ phương trình
Trong 1 ngày, đội A làm được 1/40 công việc nên đội A làm 1 minh sẽ hoàn thành công việc trong 40 ngày
Trong 1 ngày, đội B làm được 1/60 công việc nên đội A làm 1 minh sẽ hoàn thành công việc trong 60 ngày
Nhận xét:
Ở cách giải này thì chúng ta không cần đặt ẩn phụ để giải hệ phương trình
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.