Câu hỏi:
12/07/2024 31,711Cho tam giác ABC có AB=AC. Lấy điểm E trên cạnh AB, F trên cạnh AC sao cho AE=AF.
a) Chứng minh: BF=CE và tam giác BEC = tam giác CFB.
b) BF cắt CE tại I, cho biết IE=IF. Chứng minh: tam giác IBE = tam giác ICF bằng hai cách.
Câu hỏi trong đề: Bài tập tuần Toán 7 Học kì 1 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
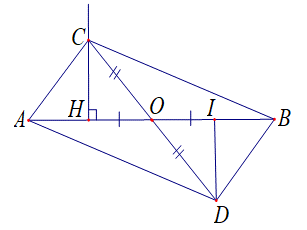
a) Xét hai tam giác vuông ΔAOC và ΔBOD ta có:
AO = BO; OC = OD (vì O là trung điểm của AB và CD)
Do đó ΔAOC = ΔBOD (hai cạnh góc vuông).
Suy ra DC = BD (hai cạnh tương ứng); \(\widehat {CAO} = \widehat {OBD}\) (hai góc tương ứng)
Mà hai góc này lại là góc so le trong nên AC // BD.
b) Xét hai tam giác vuông ΔAOD và ΔBOC ta có:
AO = BO; OC = OD (vì O là trung điểm của AB và CD)
Do đó ΔAOD = ΔBOC (hai cạnh góc vuông).
Suy ra AD = BC (hai cạnh tương ứng); \(\widehat {DAO} = \widehat {OBC}\) (hai góc tương ứng)
Mà hai góc này lại là góc so le trong nên AD // BC.
c) Xét ΔABC và ΔABD ta có:
AC = BD (cmt);
AD = BC (cmt)
AB là cạnh chung
Do đó ΔABC = ΔABD (c.c.c)
Suy ra \(\widehat {ACB} = \widehat {BDA}\) (hai góc tương ứng).
d) Xét ΔHOC và ΔIOD ta có:
OH = OI (giả thiết)
\(\widehat {HOC} = \widehat {IOD}\) (hai góc đối nhau)
OC = OD (giả thiết)
Do đó ΔHOC = ΔIOD(c.g.c)
Suy ra \(\widehat {OID} = \widehat {IHC}\)= 90° nên DI ⊥ AB.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
-
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2
Nhắn tin Zalo
Ha NhiDang
bày cho mình bài này với
Câu 16. (2,5 điểm) Cho tam giác ABC có AB>AC. Trên cạnh AB lấy điểm F sao
cho AC = AF. Gọi AD là phân giác của góc BAC. Trên cạnh AD lấy điểm E tuỳ ý.
a) So sánh góc B và góc C của tam giác ABC.
b) Chứng minh AE là đường trung trực của CF.
c) Chứng minh rằng hai lần EF nhỏ hơn chu vi của tam giác ACD.