Các lớp 6A, 6B, 6C, 6D, 6E có số học sinh tương ứng là 40, 45, 39, 44, 42. Hỏi:
a) Lớp nào có thể xếp thành 3 hàng với số học sinh ở mỗi hàng là như nhau?
b) Lớp nào có thể xếp thành 9 hàng với số học sinh ở mỗi hàng là như nhau?
c) Có thể xếp tất cả học sinh của năm lớp đó thành 3 hàng với số học sinh ở mỗi hàng là như nhau được không?
d) Có thể xếp tất cả học sinh của năm lớp đó thành 9 hàng với số học sinh ở mỗi hàng là như nhau được không?
Câu hỏi trong đề: Giải SGK Toán 6 Chương 1: Số tự nhiên - Bộ Cánh diều !!
Quảng cáo
Trả lời:
a) Để số học sinh của một lớp có thể xếp thành ba hàng với số học sinh ở mỗi hàng là như nhau thì tổng số học sinh của lớp đó phải là số chia hết cho 3.
Trong các số 40; 45; 39; 44; 42 thì:
+ Số 45 chia hết cho 3 (vì 45 có tổng các chữ số là 4 + 5 = 9 chia hết cho 3)
+ Số 39 chia hết cho 3 (vì 39 có tổng các chữ số là 3 + 9 = 12 chia hết cho 3)
+ Số 42 chia hết cho 3 (vì 42 có tổng các chữ số là 4 + 2 = 6 chia hết cho 3)
Vậy các lớp 6B, 6C; 6E có thể xếp thành 3 hàng với số học sinh ở mỗi hàng là như nhau.
b) Để số học sinh của một lớp có thể xếp thành chín hàng với số học sinh ở mỗi hàng là như nhau thì tổng số học sinh của lớp đó phải là số chia hết cho 9.
Trong các số 40; 45; 39; 44; 42 thì chỉ có số 45 chia hết cho 9 (vì 45 có tổng các chữ số là 4 + 5 = 9 chia hết cho 9).
Vậy chỉ có lớp 6B có thể xếp thành 9 hàng với số học sinh ở mỗi hàng là như nhau.
c) Tổng số học sinh của cả 5 lớp 6A, 6B, 6C, 6D, 6E là:
40 + 45 + 39 + 44 + 42 = 210 (học sinh)
Ta có số 210 là số chia hết cho 3 (vì tổng các chữ số của số 210 là 2 + 1 + 0 = 3 chia hết cho 3)
Do đó tổng số học sinh của cả 5 lớp là số chia hết cho 3.
Vậy ta có thể xếp tất cả học sinh của 5 lớp đó thành 3 hàng với số học sinh ở mỗi hàng là như nhau.
d) Ta có số 210 là số không chia hết cho 9 (vì tổng các chữ số của số 210 là 2 + 1 + 0 = 3 không chia hết cho 9)
Do đó tổng số học sinh của cả 5 lớp là số không chia hết cho 9.
Vậy ta không thể xếp tất cả học sinh của 5 lớp đó thành 9 hàng với số học sinh ở mỗi hàng là như nhau.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) n = 4 536
+ Vì số 4 536 có chữ số tận cùng là 6 nên số này chia hết cho 2 và không chia hết cho 5.
+ Số 4 536 có tổng các chữ số là 4 + 5 + 3 + 6 = 18 vừa chia hết cho 3 vừa chia hết cho 9 nên 4 536 là số chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 4 536 là 2; 3; 9.
b) n = 3 240
+ Số 3 240 có chữ số tận cùng là 0 nên số này chia hết cho cả 2 và 5.
+ Số 3 240 có tổng các chữ số là 3 + 2 + 4 + 0 = 9 vừa chia hết cho 3 vừa chia hết cho 9 nên 3 240 là số chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 3 240 là 2; 3; 5; 9.
c) n = 9 805
+ Số 9 805 có chữ số tận cùng là 5 nên số này chia hết cho 5 và không chia hết cho 2.
+ Số 9 805 có tổng các chữ số là 9 + 8 + 0 + 5 = 22 không chia hết cho cả 3 và 9 nên số 9 805 không chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 9 805 là 5.
Lời giải
a) Vì * là một chữ số trong số 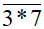 nên * phải là một trong các số: 0; 1; 2; …; 9.
nên * phải là một trong các số: 0; 1; 2; …; 9.
Số 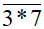 chia hết cho 3 nên tổng các chữ số của số
chia hết cho 3 nên tổng các chữ số của số 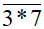 là (3 + * + 7) = (10 + *) phải là số chia hết cho 3.
là (3 + * + 7) = (10 + *) phải là số chia hết cho 3.
Thử thay * lần lượt bằng các số 0; 1; 2; …; 9, ta thấy các số thỏa mãn là 2; 5; 8.
Vậy các chữ số thích hợp điền vào dấu * để số 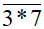 chia hết cho 3 là: 2; 5; 8.
chia hết cho 3 là: 2; 5; 8.
b) Vì * là một chữ số trong số 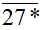 nên * phải là một trong các số: 0; 1; 2; …; 9.
nên * phải là một trong các số: 0; 1; 2; …; 9.
Số 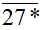 chia hết cho 9 nên tổng các chữ số của số
chia hết cho 9 nên tổng các chữ số của số 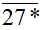 là (2 + 7 + *) = (9 + *) phải là số chia hết cho 9.
là (2 + 7 + *) = (9 + *) phải là số chia hết cho 9.
Thử thay * lần lượt bằng các số 0; 1; 2; …; 9, ta thấy các số thỏa mãn là 0; 9.
Vậy các chữ số thích hợp điền vào dấu * để số 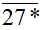 chia hết cho 9 là: 0; 9.
chia hết cho 9 là: 0; 9.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.