Khi nào thì AM + MB = AB?
Với ba điểm phân biệt A, B, M, ta có ba đoạn thẳng MA, MB, AB và MA + MB ≥ AB.
- Nếu M nằm giữa hai điểm A và B (tức là M thuộc đoạn thẳng AB) thì MA + MB = AB. Ngược lại, nếu MA + MB = AB thì điểm M nằm giữa hai điểm A và B (Hình 52).
- Nếu M không nằm giữa hai điểm A và B (tức là M không thuộc đoạn thẳng AB) thì MA + MB > AB. Ngược lại, nếu MA + MB > AB thì điểm M không nằm giữa hai điểm A và B.

Áp dụng. Bạn Bình đi từ nhà đến trường theo một đường thẳng. Trên đường đến trường, bạn Bình lần lượt đi qua nhà bạn Cường và nhà bạn Long. Khoảng cách từ nhà bạn Bình đến nhà bạn Cường là 200 m, khoảng cách từ nhà bạn Cường đến nhà bạn Long là 300 m. Khoảng cách từ nhà bạn Bình đến trường là 1 200 m. Nhà bạn Cường và nhà bạn Long cách trường bao nhiêu mét?
Câu hỏi trong đề: Giải SGK Toán 6 Chương 6. Hình học phẳng - Bộ Cánh diều !!
Quảng cáo
Trả lời:
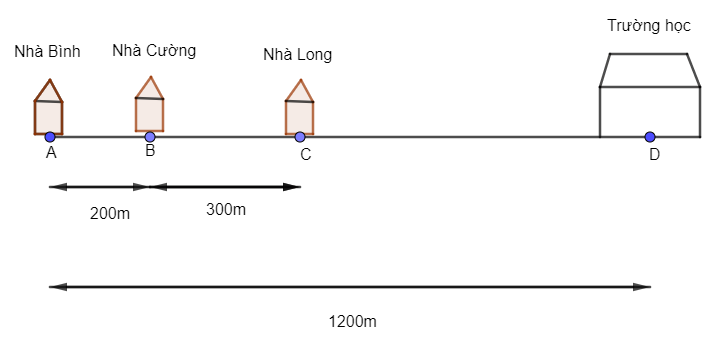
Đặt điểm A là vị trí nhà Bình, B là vị trí nhà Cường, C là vị trí nhà Long, D là vị trí trường học.
Do quãng đường từ nhà Bình đến trường lần lượt đi qua nhà bạn Cường và nhà bạn Long nên điểm B nằm giữa điểm A và điểm C. Khi đó, ta có:
AB + BC = AC
200 + 300 = AC
AC = 500.
Vì B nằm giữa A và D nên ta có AB + BD = AD
Mà AB = 200, AD = 1 200
Suy ra 200 + BD = 1 200
BD = 1 200 – 200
BD = 1 000.
Suy ra quãng đường từ nhà Cường đến trường là 1 000 m.
Ta lại có C nằm giữa A và D nên AC + CD = AD.
Mà AC = 500 m, AD = 1 200 m.
Suy ra 500 + CD = 1 200
CD = 1 200 – 500
CD = 700 m.
Suy ra quãng đường từ nhà Long đến trường là 700 m.
Vậy quãng đường từ nhà Cường đến trường là 1 000 m và quãng đường từ nhà Long đến trường là 700 m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
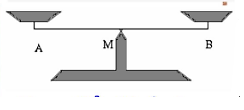
+) Bập bênh: Điểm tựa của bập bênh chính là trung điểm của thanh ngồi.

Điểm đặt trục M của cân sẽ là trung điểm của đoạn thẳng AB.
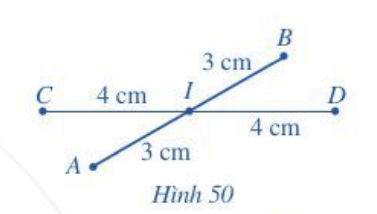
Lời giải
a) Độ dài đường gấp khúc ABCD bằng độ dài đoạn AB cộng độ dài đoạn BC cộng độ dài đoạn CD và bằng: 4 + 7 + 3 = 14 (cm).
Vậy độ dài đường gấp khúc ABCD bằng 14 cm.
b) Vì 14 > 9 nên độ dài đường gấp khúc ABCD lớn hơn độ dài đoạn thẳng AD.
Vậy độ dài đường gấp khúc ABCD lớn hơn độ dài đoạn thẳng AD.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
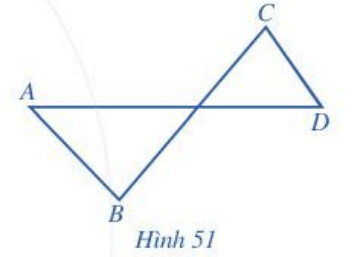
 nằm giữa hai điểm
nằm giữa hai điểm