Câu hỏi:
13/07/2024 4,123Một lớp học có 27 học sinh nam và 18 học sinh nữ. Có bao nhiêu cách chia lớp đó thành các tổ sao cho số học sinh nam và số học sinh nữ ở mỗi tổ là như nhau? Cách chia nào để mỗi tổ có số học sinh ít nhất?
Câu hỏi trong đề: Giải SBT Toán 6 Chương 1: Số tự nhiên - Bộ Cánh diều !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì số học sinh nam và số học sinh nữ ở mỗi tổ là như nhau nên số tổ sẽ là ước chung của 27 và 18.
Ta có: 27 = 33, 18 = 2.32.
Suy ra ƯCLN(27, 18) = 32 = 9.
ƯC(27, 18) = {1; 3; 9}.
Do đó ta có ba cách chia lớp thành 1 tổ, 3 tổ và 9 tổ, ta có bảng sau:
Số tổ | Số học sinh nam mỗi tổ | Số học sinh nữ mỗi tổ |
1 | 27 | 18 |
3 | 9 | 6 |
9 | 3 | 2 |
Để số học sinh trong mỗi tổ là ít nhất thì ta chia lớp đó thành 9 tổ.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Vì 24 chia hết cho 12 nên ƯCLN(12, 24) = 12.
Khi đó
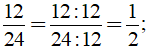
Vì 39 chia hết cho 13 nên ƯCLN(13, 39) = 13.
Khi đó
Vì 105 chia hết cho 35 nên ƯCLN(35, 105) = 35.
Khi đó
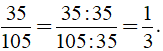
b) Ta có 120 = 23.3.5, 245 = 5.72 nên ƯCLN(120, 245) = 5.
Khi đó
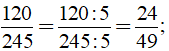
Ta có: 134 = 2.67, 402 = 2.3.67 nên ƯCLN(134, 402) = 2.67 = 134.
Khi đó
Ta có 852 chia hết cho 213 nên ƯCLN(213, 852) = 213.
Khi đó
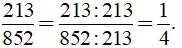
c) Vì 1 170 = 234.5 nên chia hết cho 234. Do đó ƯCLN(234, 1 170) = 234.
Khi đó
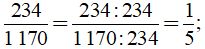
Vì 3 663 = 1 221.3 nên chia hết cho 1 221. Do đó ƯCLN(1 221, 3 663) = 1 221.
Khi đó
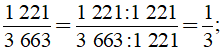
Vì 31 995 = 2 133.15 nên chia hết cho 2 133. Do đó ƯCLN(31 995, 2 133) = 2 133.
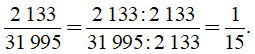
Lời giải
a) Ta có 15 = 3.5, 105 = 3.5.7
Khi đó Ư CLN(15, 105) = 3.5 = 15
Suy ra ƯC(15, 105) = Ư(15) = {1; 3; 5; 15}.
Vậy trong các số đã cho các số là ước chung của 15 và 105 là: 1; 5; 15.
b) Ta có: 27 = 33, 156 = 22.3.13.
Khi đó ƯCLN(27, 156) = 3.
Vậy ƯCLN(27, 156) = 3.
c) Ta có: 106 = 2.53, 318 = 2.3.53.
Khi đó ƯCLN(106, 318) = 2.53 = 106.
Ta có: 424 = 106.4, 636 =2.318.
Mà ƯCLN(106, 318) = 2.53 = 106 nên ƯCLN(424, 636) = 2.106 = 212.
Suy ra ƯC(424, 636) = Ư(212) = {1; 2; 4; 53; 106; 212}.
Vậy ƯC(424, 636) = {1; 2; 4; 53; 106; 212}.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
10 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 1: Tập hợp. Phần tử của tập hợp (có đáp án)
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 11
-
Dạng 1. Biểu diễn một tập hợp cho trước
-
5 câu Trắc nghiệm Toán 6 Cánh diều Bài 1: Tập hợp có đáp án ( Nhận biết )
Nhắn tin Zalo