Tìm các số tự nhiên a, b, biết:
a) a + b = 192 và ƯCLN(a, b) = 24;
b) ab = 216 và ƯCLN(a, b) = 6.
Câu hỏi trong đề: Giải SBT Toán 6 Chương 1: Số tự nhiên - Bộ Cánh diều !!
Quảng cáo
Trả lời:
a) Vì ƯCLN(a, b) = 24 nên a = 24p, b = 24q với p, q là các số tự nhiên và nguyên tố cùng nhau.
Thay a = 24p và b = 24q vào biểu thức a + b = 192 ta được:
24p + 24q = 192
24(p + q) = 192
P + q = 8.
Do p, q là các số tự nhiên và nguyên tố cùng nhau nên ta có các cặp (p; q) tương ứng là: (1; 7), (7; 1), (3; 5), (5; 3).
+) Với p = 1, q = 7 thì a = 24, b = 168;
+) Với p = 7, q = 1 thì a = 168, b = 24;
+) Với p = 3, q = 5 thì a = 72, b =120;
+) Với p = 5, q = 3 thì a = 120, b = 72.
Vậy ta có các cặp (a, b) là: (168; 24), (24; 168), (72; 120), (120; 72).
b) Vì ƯCLN(a, b) = 6 nên a = 6p, b = 6q với p, q là các số tự nhiên và nguyên tố cùng nhau.
Thay a = 6p và b = 6q vào biểu thức ab = 216 ta được:
6p.6q = 216
36pq = 216
pq = 6.
Do p, q là các số tự nhiên và nguyên tố cùng nhau nên ta có các cặp (p; q) tương ứng là: (1; 6), (6; 1), (3; 2), (2; 3).
+) Với p = 1, q = 6 thì a = 6.1 = 6, b = 6.6 = 36;
+) Với p = 6, q = 1 thì a = 6.6 = 36, b = 6.1 = 6;
+) Với p = 3, q = 2 thì a = 6.3 = 18, b = 6.2 = 12;
+) Với p = 2, q = 3 thì a = 6.2 = 12, b = 6.3 = 18.
Vậy ta có các cặp (a, b) là: (6; 36), (36; 6), (18; 12), (18; 12).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Vì 24 chia hết cho 12 nên ƯCLN(12, 24) = 12.
Khi đó
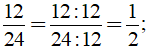
Vì 39 chia hết cho 13 nên ƯCLN(13, 39) = 13.
Khi đó

Vì 105 chia hết cho 35 nên ƯCLN(35, 105) = 35.
Khi đó
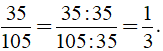
b) Ta có 120 = 23.3.5, 245 = 5.72 nên ƯCLN(120, 245) = 5.
Khi đó
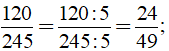
Ta có: 134 = 2.67, 402 = 2.3.67 nên ƯCLN(134, 402) = 2.67 = 134.
Khi đó

Ta có 852 chia hết cho 213 nên ƯCLN(213, 852) = 213.
Khi đó
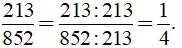
c) Vì 1 170 = 234.5 nên chia hết cho 234. Do đó ƯCLN(234, 1 170) = 234.
Khi đó
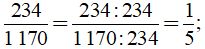
Vì 3 663 = 1 221.3 nên chia hết cho 1 221. Do đó ƯCLN(1 221, 3 663) = 1 221.
Khi đó
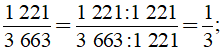
Vì 31 995 = 2 133.15 nên chia hết cho 2 133. Do đó ƯCLN(31 995, 2 133) = 2 133.
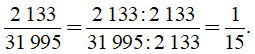
Lời giải
Vì số học sinh nam và số học sinh nữ ở mỗi tổ là như nhau nên số tổ sẽ là ước chung của 27 và 18.
Ta có: 27 = 33, 18 = 2.32.
Suy ra ƯCLN(27, 18) = 32 = 9.
ƯC(27, 18) = {1; 3; 9}.
Do đó ta có ba cách chia lớp thành 1 tổ, 3 tổ và 9 tổ, ta có bảng sau:
Số tổ | Số học sinh nam mỗi tổ | Số học sinh nữ mỗi tổ |
1 | 27 | 18 |
3 | 9 | 6 |
9 | 3 | 2 |
Để số học sinh trong mỗi tổ là ít nhất thì ta chia lớp đó thành 9 tổ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.