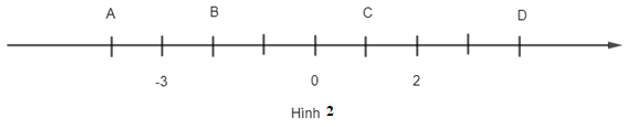
a) Các điểm A, B, C, D trên trục số ở Hình 2 biểu diễn những số nguyên nào?
b) Hãy điền tên E, F, G, H, I lần lượt cho các điểm biểu diễn các số nguyên – 5; - 4; - 2; 3; 5 trên trục số ở Hình 3.
c) Ghi điểm gốc 0 vào trục số ở Hình 4.
Câu hỏi trong đề: Giải SBT Toán 6 Chương 2: Số nguyên - Bộ Cánh diều !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Quan sát trục số, ta thấy:
Điểm A nằm liền trước điểm – 3 nên điểm A biểu diễn cho số nguyên – 4;
Điểm B nằm liền sau điểm – 3 nên điểm B biểu diễn cho số nguyên – 2;
Điểm C nằm liền sau điểm 0 nên điểm C biểu diễn cho số nguyên 1;
Điểm D nằm sau điểm 2 và cách điểm 2 hai đơn vị nên điểm D biểu diễn cho số nguyên 4.
b) Sau khi điền các điểm E, F, G, H, I , ta được trục số sau:
c) Ta có điểm – 3 cách gốc tọa độ 0 ba đơn vị về bên trái hay điểm 0 cách điểm – 3 ba đơn vị về bên phải. Khi đó ta có hình vẽ biểu diễn điểm 0 như sau:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
:Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Vì 7 là số tự nhiên nên 7 thuộc tập N, ta viết 7 
N
b) – 12 là số nguyên âm nên không thuộc tập N, ta viết -12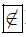 
N
c) Vì 0 là số nguyên nên 0 thuộc tập Z, ta viết 0 
Z
d) – 2 222 là số nguyên âm nên thuộc tập Z, ta viết -2 222 
Z
e) Vì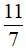 
không là số nguyên nên 
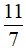không thuộc tập Z, ta viết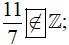 
f) Vì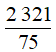 
không là số nguyên nên 
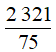không thuộc tập Z, ta viết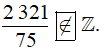 
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
+) Số đối của – 54 là 54;
+) Số đối của – 432 là 432;
+) Số đối của – 1 234 là 1 234;
+) Số đối của 767 là – 767;
+) Số đối của 8 765 là – 8 765;
+) Số đối của 100 000 là – 100 000.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
DK1 là cụm Dịch vụ kinh tế - Khoa học kĩ thuật được xây dựng dưới các nhà giàn trên thềm lục địa Việt Nam. Một nhà giàn DK1 có ba tầng trên mặt nước và ba tầng hệ thống chân đỡ dưới mặt nước có độ cao như sau:
Bộ phận nhà giàn | Độ cao |
Phần 3 chân đỡ | Dưới mực nước biển 15 m |
Phần 2 chân đỡ | Dưới mực nước biển 9 m |
Phần 1 chân đỡ | Dưới mực nước biển 4 m |
Tầng 1 | Trên mực nước biển 8 m |
Tầng 2 | Trên mực nước biển 18 m |
Tầng 3 | Trên mực nước biển 25 m |
Sử dụng số nguyên để biểu thị các độ cao đó (so với mực nước biển).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập