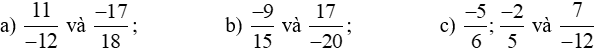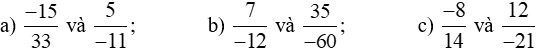Câu hỏi trong đề: Giải SBT Toán 6 Chương 5: Phân số - Bộ Chân trời sáng tạo !!
Quảng cáo
Trả lời:
Lời giải:
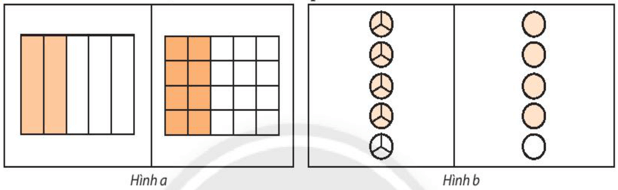
Trong hình a:
- Ở hình vẽ thứ nhất: hình chữ nhật được chia thành 5 phần bằng nhau, tô màu 2 phần. Nên phân số biểu thị số phần tô màu là 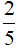 .
.
- Ở hình vẽ thứ hai: hình chữ nhật được chia thành 20 phần bằng nhau, tô màu 8 phần. Nên phân số biểu thị số phần tô màu là 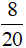 .
.
Do đó hai phân số thể hiện phần tô màu trong Hình a là 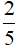 và
và 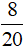 .
.
Vì 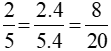 nên hình a minh hoạ tính chất 1 (Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho).
nên hình a minh hoạ tính chất 1 (Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho).
Trong hình b:
- Ở hình vẽ thứ nhất: có 5 hình tròn bằng nhau, mỗi hình tròn chia thành 3 phần bằng nhau. Trong hình trên chia thành 15 phần, tô màu 12 phần. Nên phân số biểu thị số phần tô màu là 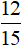 .
.
- Ở hình vẽ thứ hai: có 5 hình tròn bằng nhau, tô màu 4 hình. Nên phân số biểu thị số phần tô màu là 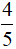 .
.
Do đó hai phân số biểu thị phần tô màu trong hình b là 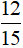 và
và 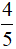 .
.
Vì 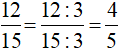 nên hình b minh hoạ tính chất 2 (Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho).
nên hình b minh hoạ tính chất 2 (Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
a) 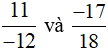
Ta có MSC = BCNN (12, 18) = 36.
Ta quy đồng như sau:
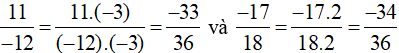
b) 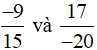
Ta có MSC = BCNN(15, 20) = 36.
Ta quy đồng như sau:
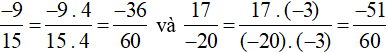
c) 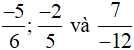
Ta có MSC = BCNN(6, 5, 12) = 60.
Ta quy đồng như sau:
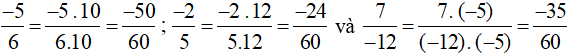
Lời giải
Lời giải:
Ta thực hiện theo hai bước như sau:
Bước 1: Tìm mẫu số chung của hai phân số (là bội chung nhỏ nhất của các mẫu số).
Bước 2: Nhân cả tử và mẫu của mỗi phân số với số nguyên thích hợp (nhân tử phụ) để được phân số mới có mẫu là mẫu số chung.
a) 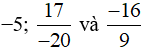
Ta có: 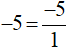
Vì BCNN(1, 20, 9) = BCNN(20, 9)
Để tìm mẫu số chung là số dương nhỏ nhất (hay là bội chung nhỏ nhất của các mẫu số) ta làm như sau:
+ Phân tích các số sau ra thừa số nguyên tố: 20 = 22.5 ; 9 = 32;
+ Thừa số nguyên tố chung và riêng là: 2; 3 và 5;
+ Số mũ lớn nhất của 2 là 2, số mũ lớn nhất của 3 là 2 và số mũ lớn nhất của 5 là 1.
+ BCNN (1; 20; 9) = 22.32.5 = 180.
Do đó mẫu số chung là số dương nhỏ nhất là 180.
Ta thực hiện:
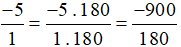
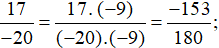
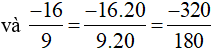
b) 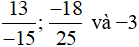
Ta có: 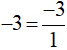
Vì BCNN(15, 25, 1) = BCNN(15, 25)
Để tìm mẫu số chung là số dương nhỏ nhất (hay là bội chung nhỏ nhất của các mẫu số) ta làm như sau:
+ Phân tích các số sau ra thừa số nguyên tố: 15 = 3.5; 25 = 52;
+ Thừa số nguyên tố chung là 5 và riêng là 3;
+ Số mũ lớn nhất của 3 là 1 và số mũ lớn nhất của 5 là 2;
+ BCNN (1; 15; 25) = 3.52 = 75.
Do đó mẫu số chung là số dương nhỏ nhất là 75.
Ta thực hiện:
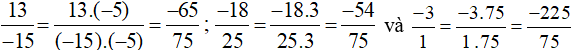
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.