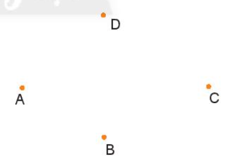
Cho bốn điểm A, B, C, D như hình vẽ bên. Có bao nhiêu tia được tạo thành nếu mỗi tia đều chứa hai trong số các điểm đó?
Quảng cáo
Trả lời:
Lời giải:
- Chọn điểm A làm điểm gốc thì có thể vẽ được 3 tia AB, AC và AD.
- Chọn điểm B làm điểm gốc thì có thể vẽ được 3 tia BA, BC và BD.
- Chọn điểm C làm điểm gốc thì có thể vẽ được 3 tia CA, CB và CD.
- Chọn điểm D làm điểm gốc thì có thể vẽ được 3 tia DA, DB và DC.
Vậy từ bốn điểm A, B, C, D có 12 tia được tạo thành (mỗi tia chứa hai trong số các điểm đó) là: AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB, DC.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
Giả sử ba điểm phân biệt không thẳng hàng là A, B, C.
Cách vẽ:
- Lấy ba điểm A, B, C không thẳng hàng.
- Vẽ đường thẳng d đi qua B, C.
- Vẽ đường thẳng đi qua A và song song với đường thẳng BC bằng eke.
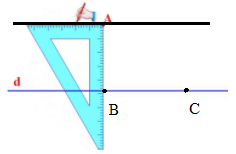
Ta có hình vẽ sau:
Lời giải
Lời giải:
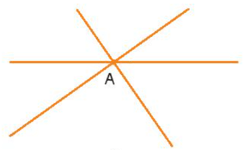
Vẽ hai đường thẳng cắt nhau tại A, ta có ba trường hợp sau:
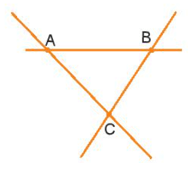
- Trường hợp 1: Đường thẳng thứ ba cắt cả hai đường thẳng kia và đi qua giao điểm A thì ta có một giao điểm A (như hình vẽ).
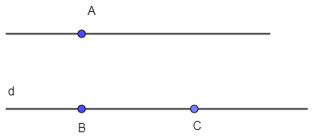
- Trường hợp 2: Đường thẳng thứ ba cắt cả hai đường thẳng kia và không đi qua giao điểm A thì ta có ba giao điểm A, B và C (như hình vẽ).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.