Câu hỏi:
20/07/2022 526Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có:
\[\frac{x}{5} = \frac{3}{y}\]⇒ x.y = 5.3 = 15
Mà 15 = 5.3 = 15.1 = (−3).(−5) = (−1).(−15)
và x,y ∈ Z, x >y nên (x;y) ∈ {(5;3), (15;1), (−3;−5), (−1;−15)}
Đáp án cần chọn là: A
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vì C∈N nên C∈Z. Do đó ta tìm n∈Z để C∈Z
Vì n∈Z nên để C∈Z thì 2n+1∈U(11) = {±1; ±11}
Ta có bảng:
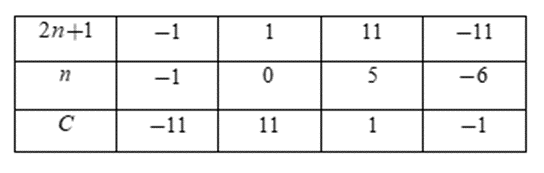
Vì C∈N nên ta chỉ nhận các giá trị n = 0; n = 5
Đáp án cần chọn là: C
Lời giải
Ta có: x – y = 5 ⇒ x = y + 5 thay vào \[\frac{{x - 4}}{{y - 3}} = \frac{4}{3}\]ta được:
\[\frac{{y + 5 - 4}}{{y - 3}} = \frac{4}{3}\]
\[\frac{{y + 1}}{{y - 3}} = \frac{4}{3}\]
3(y + 1) = 4(y − 3)
3y + 3 = 4y − 12
3y − 4y = −12 − 3
−y = −15
y = 15
⇒ x = 15 + 5 = 20
Vậy x = 20; y = 15
Đáp án cần chọn là: C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
10 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 1: Tập hợp. Phần tử của tập hợp (có đáp án)
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 11
-
Dạng 1. Biểu diễn một tập hợp cho trước
-
Đề thi Toán 6 Học kì 2 có đáp án (Đề 11)