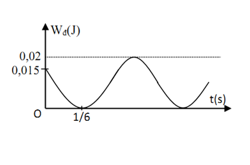
Một vật có khối lượng 400g dao động điều hòa có đồ thị động năng như hình vẽ. Tại thời điểm t = 0 vật đang chuyển động theo chiều dương, lấy \({\pi ^2} = 10\). Phương trình dao động của vật là:
A.\[x = 10c{\rm{os}}\left( {2\pi t + \frac{\pi }{3}} \right)cm\]
B. \[x = 10c{\rm{os}}\left( {2\pi t - \frac{\pi }{3}} \right)cm\]
C. \[x = 5c{\rm{os}}\left( {2\pi t + \frac{\pi }{3}} \right)cm\]
D. \[x = 5c{\rm{os}}\left( {2\pi t - \frac{\pi }{3}} \right)cm\]
Câu hỏi trong đề: ĐGNL ĐHQG Hà Nội - Khoa học tự nhiên - Con lắc lò xo !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Từ đồ thị, ta có:
+ Tại thời điểm ban đầu (t =0) :
\[{{\rm{W}}_d} = 0,015 \to {{\rm{W}}_t} = 0,02 - 0,015 = {5.10^{ - 3}}J = \frac{{\rm{W}}}{4}\]
\[ \to {x_0} = \pm \frac{A}{2}\]
+ Vị trí có Wđ= 0 lần thứ nhất: <=>x1= ±A
Dựa vào đồ thị ta suy ra: x0= A/2 và x1= A
=>Khoảng thời gian vật đi từ x0đến x1là:
\[{\rm{\Delta }}t = \frac{T}{6} = \frac{1}{6}s \to T = 1{\rm{s}} \to \omega = \frac{{2\pi }}{T} = 2\pi (ra{\rm{d}}/s)\]
\[{{\rm{W}}_{{{\rm{d}}_{{\rm{max}}}}}} = \frac{1}{2}m{\omega ^2}{A^2} = 0,02 \to A = \sqrt {\frac{{2{{\rm{W}}_{{d_{{\rm{max}}}}}}}}{{m{\omega ^2}}}} = \sqrt {\frac{{2.0,02}}{{0,4.{{(2\pi )}^2}}}} = 0,05m = 5cm\]
Tại t = 0:
\(\left\{ {\begin{array}{*{20}{c}}{{x_0} = Acos\varphi = \frac{A}{2}}\\{v = - Asin\varphi >0}\end{array}} \right. \to \left\{ {\begin{array}{*{20}{c}}{cos\varphi = \frac{1}{2}}\\{sin\varphi < 0}\end{array}} \right. \to \varphi = - \frac{\pi }{3}\)
=>Phương trình dao động của vật:\[x = 5c{\rm{os}}\left( {2\pi t - \frac{\pi }{3}} \right)cm\]
Đáp án cần chọn là: D
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[A.\sqrt {\frac{k}{m}} .\]
B. \[\frac{{Am}}{k}.\]
C. \[A\sqrt {\frac{m}{k}} .\]
D. \[\frac{{Ak}}{m}.\]Trả lời:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Tốc độ góc của con lắc: \[\omega = \sqrt {\frac{k}{m}} \]
Tốc độ cực đại của vật là \[{v_{{\rm{max}}}} = \omega A = A.\sqrt {\frac{k}{m}} \]
Chọn đáp án A
Câu 2
A.\[x = \pm \frac{{A\omega }}{{\sqrt {n + 1} }},v = \pm A\sqrt {\frac{n}{{n + 1}}} \]
B. \[x = \pm A\sqrt {n + 1} ,v = \pm A\omega \sqrt {\frac{n}{{n + 1}}} \]
C. \[x = \pm \frac{A}{{\sqrt {n + 1} }},v = \pm A\omega \sqrt {\frac{n}{{n + 1}}} \]
D. \[x = \pm A\sqrt {\frac{n}{{n + 1}}} ,v = \pm \frac{{A\omega }}{{\sqrt {n + 1} }}\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Tại vị trí có động năng gấp n lần thế năng của vật: Wđ = nWt
\(\left\{ {\begin{array}{*{20}{c}}{{W_d} = n{W_t}}\\{W = {W_t} + {W_d}}\end{array}} \right. \to \left\{ {\begin{array}{*{20}{c}}{{W_t} = \frac{1}{{n + 1}}W}\\{{W_d} = \frac{n}{{n + 1}}W}\end{array}} \right.\)
\( \to \left\{ {\begin{array}{*{20}{c}}{x = \pm \frac{A}{{\sqrt {n + 1} }}}\\{v = \pm A\omega \sqrt {\frac{n}{{n + 1}}} }\end{array}} \right.\)
Đáp án cần chọn là: C
Câu 3
A.4T.
B.T.
C.\(\frac{T}{2}\)
D.2T.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.Đồ thị A
B.Đồ thị B
C.Đồ thị C
D.Đồ thị D
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.90g.
B.70g.
C.110g.
D.50g.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.Gia tốc của sự rơi tự do.
B.Biên độ của dao động.
C.Điều kiện kích thích ban đầu.
D.Khối lượng của vật nặng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
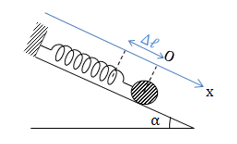
Câu 7
A.\[{\rm{\Delta }}l = \frac{{mg\sin \alpha }}{k};T = 2\pi \sqrt {\frac{{{\rm{\Delta }}l}}{{g\sin \alpha }}} \]
B. \[{\rm{\Delta }}l = \frac{k}{{mg\sin \alpha }};T = 2\pi \sqrt {\frac{{{\rm{\Delta }}l}}{{g\sin \alpha }}} \]
C. \[{\rm{\Delta }}l = \frac{{mg\sin \alpha }}{k};T = \frac{1}{{2\pi }}\sqrt {\frac{{g\sin \alpha }}{{{\rm{\Delta }}l}}} \]
D. \[{\rm{\Delta }}l = \frac{k}{{mg\sin \alpha }};T = \frac{1}{{2\pi }}\sqrt {\frac{{{\rm{\Delta }}l}}{{g\sin \alpha }}} \]Trả lời:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập