ĐGNL ĐHQG Hà Nội - Khoa học tự nhiên - Phóng xạ

A, B, C - đúng

D -sai vì: Hằng số phóng xạ \[\lambda = \frac{{\ln 2}}{T}\]

Đáp án cần chọn là: D

Ta có:

+ Số hạt nhân phóng xạ còn lại: \[N = {N_0}{2^{ - \frac{t}{T}}}\]

+ Số mol chất phóng xạ còn lại: \[{n_{(t)}} = \frac{{{m_{(t)}}}}{A} = \frac{{{m_0}{{.2}^{ - \frac{t}{T}}}}}{A}\]

+ Khối lượng của chất đã phân rã: \[{\rm{\Delta }}m = {m_0}(1 - {2^{ - \frac{t}{T}}})\]

+ Độ phóng xạ của lượng chất còn lại: \[H = \frac{{{H_0}}}{{{2^{\frac{t}{T}}}}} = {H_0}{.2^{ - \frac{t}{T}}}\]

=>Khối lượng của lượng chất đã phân rã không biến thiên cùng quy luật với các đại lượng còn lại

Đáp án cần chọn là: C

Khối lượng Co còn lại sau 10,66 năm là:

\[m = {m_0}{.2^{ - \frac{t}{T}}} = {1000.2^{ - \frac{{10,66}}{{5,33}}}} = 250g\]

Số nguyên tử Coban còn lại là:

\[N = \frac{m}{A}.{N_A} = \frac{{250}}{{60}}{.6,02.10^{23}} = {2,51.10^{24}}\]

Đáp án cần chọn là: A

Số hạt nhân mẹ còn lại sau thời gian t được xác định bởi:  \[N = {N_0}{.2^{\frac{{ - t}}{T}}}\]

Số hạt nhân con được tạo thành hay số hạt nhân mẹ đã bị phân rã sau thời gian t được xác định bởi:

\[\begin{array}{*{20}{l}}{N' = {N_0} - N = {N_0}.(1 - {2^{\frac{{ - t}}{T}}}) = 70{\rm{\% }}{N_0}}\\{ \Rightarrow (1 - {2^{\frac{{ - t}}{T}}}) = 70{\rm{\% }} = 0,7 \Rightarrow {2^{\frac{{ - t}}{T}}} = 0,3}\\{ \Rightarrow t = - T.{{\log }_2}(0,3) = 1,74T = 1,74.3,8 = 6,6}\end{array}\]

Vậy thời gian là 6,6 ngày.

Đáp án cần chọn là: A

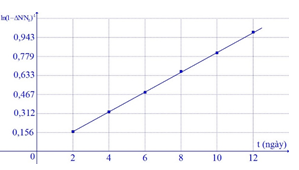
Ta có: \[N = {N_0}{e^{ - \lambda t}} \Rightarrow \] Số hạt bị phân rã là:

\[{\rm{\Delta }}N = {N_0} - {N_0}{e^{ - \lambda t}} = {N_0}(1 - {e^{ - \lambda t}})\]

\[ \Rightarrow \frac{{{\rm{\Delta }}N}}{{{N_0}}} = 1 - {e^{ - \lambda t}} \Rightarrow 1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}} = {e^{ - \lambda t}}\]

\[ \Rightarrow \frac{1}{{\left( {1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}}} \right)}} = {e^{\lambda t}} \Rightarrow \ln {\left( {1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}}} \right)^{ - 1}} = \lambda t\]

Từ đồ thị ta thấy \[\lambda \approx 0,078\]

\[ \Rightarrow T = \frac{{\ln 2}}{\lambda } \approx 8,9\]Đáp án cần chọn là: B