Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
134 người thi tuần này 4.6 5.6 K lượt thi 150 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
Câu 1
Lời giải
Câu 2
Lời giải
Số ngày bạn An để dành tiền (thời gian bỏ ống heo tính từ ngày 01 tháng 01 năm 2016 đến ngày 30 tháng 4 năm 2016) là \(31 + 29 + 31 + 30 = 121\) (ngày)
Số tiền bỏ ống heo ngày đầu tiên là \({u_1} = 100.\)
Số tiền bỏ ống heo ngày thứ hai là \({u_2} = 100 + 1.100.\)
Số tiền bỏ ống heo ngày thứ ba là \({u_3} = 100 + 2.100.\)
Số tiền bỏ ống heo ngày thứ \(n\) là \({u_n} = {u_1} + \left( {n - 1} \right)d = 100 + \left( {n - 1} \right) \cdot 100 = 100n\)
Số tiền bỏ ống heo ngày thứ 121 là \({u_{121}} = 100 \cdot 121 = 12\,\,100\).
Sau 121 ngày thì số tiền An tích luỹ được là tổng của 121 số hạng đầu của cấp số cộng có số hạng đầu \({u_1} = 100\,;\,\,d = 100.\)
Vậy số tiền An tích luỹ được là:
\({S_{121}} = \frac{{121}}{2}\left( {{u_1} + {u_{121}}} \right) = \frac{{121}}{2}\left( {100 + 12\,\,100} \right) = 738\,\,100\) (đồng). Chọn A.
Câu 3
Lời giải
Ta có \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {AB} = \left( { - 1\,;\,\,2\,;\,\, - 3} \right)}\\{\overrightarrow {BC} = \left( { - 7\,;\,\, - 5\,;\,\, - 1} \right)}\end{array} \Rightarrow \overrightarrow {AB} \cdot \overrightarrow {BC} = \vec 0 \Rightarrow } \right.\) tam giác \[ABC\] vuông tại \[B.\]
\( \Rightarrow \) Tâm \(I\) của đường tròn ngoại tiếp tam giác \[ABC\] là trung điểm của cạnh huyền \[AC.\]
\( \Rightarrow I\left( {1\,;\,\, - \frac{1}{2}\,;\,\,3} \right).\)
Vậy \(a + 2b + c = 3.\) Chọn B.
Câu 4
Lời giải
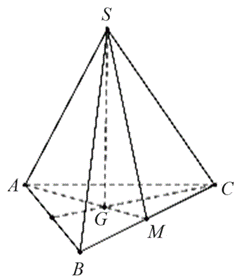
Gọi \(G\) là tâm của tam giác đều \[ABC\] và \(M\) là trung điểm của \[BC.\]
Theo giả thiết góc giữa mặt bên và đáy bằng \(45^\circ \) suy ra \(\widehat {SMG} = 45^\circ .\)
Tam giác \[ABC\] đều cạnh \(a\) nên \(AM = \frac{{\sqrt 3 }}{2}a\) và \(GM = \frac{1}{3}AM = \frac{{a\sqrt 3 }}{6}.\)Xét tam giác \[SGM\] có: \(\tan \widehat {SMG} = \frac{{SG}}{{GM}} \Leftrightarrow \tan 45^\circ = \frac{{SG}}{{GM}} \Rightarrow SG = GM = \frac{{a\sqrt 3 }}{6}\).
Vậy thể tích khối chóp \(S.ABC\) là: \({V_{S \cdot ABC}} = \frac{1}{3} \cdot {S_{ABC}} \cdot SG = \frac{1}{3} \cdot \frac{{\sqrt 3 }}{4}{a^2} \cdot \frac{{a\sqrt 3 }}{6} = \frac{{{a^3}}}{{24}}.\)
Chọn B.
Lời giải
Ta có \({z^2} - 4z + 13 = 0 \Leftrightarrow {\left( {z - 2} \right)^2} = - 9\)
\( \Leftrightarrow {\left( {z - 2} \right)^2} = {\left( {3i} \right)^2} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{z = 2 + 3i}\\{z = 2 - 3i}\end{array} \Rightarrow A\left( {2\,;\,\,3} \right),\,\,B\left( {2\,;\,\, - 3} \right)} \right.{\rm{. }}\)
Ta có \(OA = OB = \sqrt {13} \). Do đó \(\Delta OAB\) cân tại O.
Gọi \(H\) là trung điểm của \(AB\) nên \(H\left( {2\,;\,\,0} \right)\) và \(OH \bot AB,\,\,OH = 2,\,\,AB = 6.\)
Vậy \({S_{OAB}} = \frac{1}{2}OH \cdot AB = \frac{1}{2} \cdot 2 \cdot 6 = 6.\) Chọn D.
Câu 6
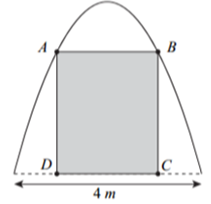
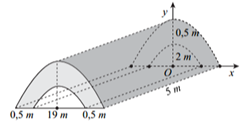
A. \(37,5\,\;{\rm{m}}.\)
B. \(112,5\;\,{\rm{m}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(\left( {1\,;\,\,2} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
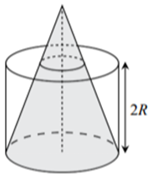
A. \(V = 1,27\;\,{{\rm{m}}^3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
A. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = {25^2}.\)
B. \({\left( {x + 2} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z + 4} \right)^2} = {25^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
A. hân hạnh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
A. thoát li.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
A. văn minh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 55
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 56
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 60
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 61
A. nhập khẩu - khó khăn.
B. buôn bán - thuận tiện.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
A. vị nghệ thuật.
B. nghị luận mẫu mực.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
A. cách mạng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 64
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 65
A. khối lượng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 66
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 67
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 68
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 69
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 70
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 71
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 72
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 73
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 75
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 76
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 77
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 78
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 79
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 80
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 81
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 83
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 85
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 87
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 89
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 91
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 92
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 95
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 96
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
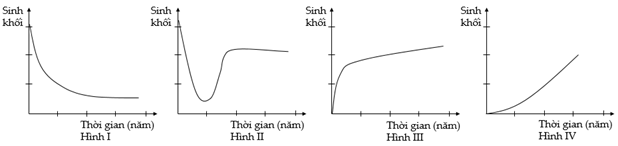
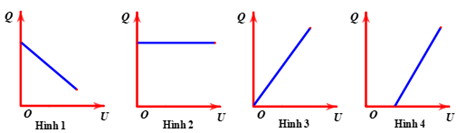
Câu 98
A. Hình 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 99
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 100
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 102
A. 430 Hz.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 103
A. 1,75 kg.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 104
A. \[3\pi {.10^3}{\mkern 1mu} {\mkern 1mu} m.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 105
D. Tia \(\gamma \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
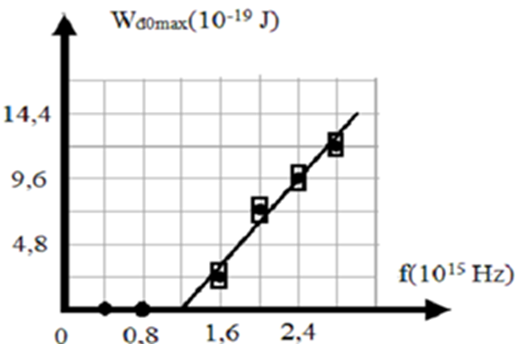
Câu 106
A. \({4.10^{ - 34}}J.s\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 108
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 110
A. 28,14%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 112
A. 150 ml.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 113
A. 70%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
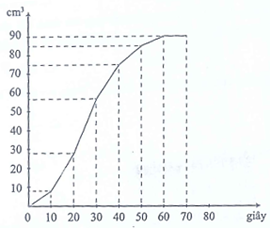
Câu 115
A. 40 giây.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 116
A. 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 118
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 119
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 120
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 121
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 122
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 123
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 124
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 125
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 126
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Đọc đoạn trích sau và trả lời các câu hỏi từ 51 đến 55:
Hầu hết mọi người có thể nhớ một số điện thoại trong tối đa ba mươi giây. Tuy nhiên, khi khoảng thời gian ngắn này trôi qua, các dữ liệu sẽ bị xóa khỏi bộ nhớ. Làm thế nào để ghi nhớ các thông tin ngay từ lần đầu tiên ?
Thông tin đi đến bộ nhớ ngắn hạn sẽ thông qua hệ thống giác quan. Bộ não có một bộ lọc cho phép các thông tin cần ghi nhớ ngay lập tức truyền đến bộ nhớ ngắn hạn. Các nhà nghiên cứu cho rằng người ta có thể tăng dung lượng của trí nhớ ngắn hạn bằng cách phân chia hoặc phân loại các thông tin tương tự với nhau. Bằng cách sắp xếp thông tin, người ta có thể tối ưu hóa bộ nhớ ngắn hạn và cải thiện khả năng của bộ nhớ, từ đó chuyển sang bộ nhớ dài hạn.
Khi cố gắng ghi nhớ điều gì đó, chẳng hạn kiến thức cho một kì thi, nhiều người lựa chọn phương pháp học thuộc lòng, có nghĩa là đọc to, lặp đi lặp lại kiến thức đó, cố gắng lưu giữ khối lượng kiến thức đó tồn tại thật lâu trong trí nhớ. Tuy nhiên, kiểu học thuộc này chỉ thành công khi không có sự gián đoạn. Ngay sau khi người học ngừng lặp lại thông tin, thông tin đó sẽ nhanh chóng biến mất. Khi cần lưu lại một số điện thoại mà không có giấy và bút, mọi người thường cố gắng ghi nhớ bằng cách đọc lặp đi lặp lại số điện thoại đó. Nhưng nếu có người bấm chuông cửa hoặc có tiếng chó sủa, anh ta có thể sẽ ngay lập tức quên mất số điện thoại đang cố gắng ghi nhớ. Do đó, học thuộc lòng không phải là một cách hiệu quả để truyền thông tin từ trí nhớ ngắn hạn sang trí nhớ dài hạn. Một cách tốt hơn để ghi nhớ đó là mã hóa thông tin, có nghĩa là gán ý nghĩa hoặc hình ảnh cho thông tin đó để nó có thể được lưu trữ cùng với những kí ức dài hạn khác đã tồn tại từ trước.
Mã hóa thông tin cũng khiến cho thông tin dễ được truy xuất hơn. Việc truy xuất thông tin có thể được thực hiện bằng cách ghi nhận hoặc thu hồi. Con người có thể dễ dàng nhớ lại những kí ức được lưu trữ trong bộ nhớ dài hạn và được sử dụng thường xuyên. Nếu một kí ức vô tình bị lãng quên thì cũng có thể lấy lại được bằng cách nhắc nhở. Một người có thể chuyển hóa thông tin về dạng hình ảnh, kí hiệu thì khả năng khôi phục kí ức càng cao. Đây là lí do tại sao các bài kiểm tra trắc nghiệm thường được sử dụng cho các môn học yêu cầu ghi nhớ nhiều.
(Sưu tầm)
Câu 128
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 129
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 130
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 131
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 56 đến 60:
Vi nhựa trong cơ thể con người: Chúng sẽ hủy hoại chúng ta?
Các nhà khoa học đang nghiên cứu mở rộng về độc chất trong nhựa cũng như các bệnh về phổi, từ các bệnh về đường hô hấp đến ung thư, vốn là nguyên nhân dẫn đến cái chết của hàng triệu người mỗi năm và có liên quan đến việc phơi nhiễm nhiều chất ô nhiễm khác. Hiệp hội Phổi Mỹ, trong báo cáo mới nhất cho biết viêm mãn tính là một trong bốn nguyên nhân dẫn đến cái chết ở Mỹ.
Con người hít vào vô số các hạt ngoại lai mỗi ngày, kể từ buổi bình minh của Cách mạng Công nghiệp. Phản hồi đầu tiên của cơ thể là tìm cách để tống khứ chúng. Những hạt lớn hơn theo đường thở thuộc dạng như vậy khi ho. Niêm dịch hình thành quanh các hạt đưa chúng xuống đường hô hấp, tạo ra một dạng “thang máy” niêm dịch tống chúng ngược trở ra đường hô hấp trên. Các tế bào miễn dịch xung quanh để cô lập chúng. Theo thời gian, những hạt này có thể làm kích thích và dẫn đến nhiều triệu chứng từ viêm nhiễm đến lây nhiễm và cuối cùng là ung thư. Hoặc chúng có thể chỉ hiện diện như một vật trơ và không làm điều gì ghê gớm.
Nhưng các hạt trong nghiên cứu về phổi đều từ nhựa và được biết là độc hại với người, là nguyên nhân của kích thích phổi, hoa mắt, chóng mặt, đau đầu và ung thư, Kari Nadeau, một nhà nghiên cứu về dị ứng và bệnh hen suyễn ở ĐH Stanford. “Chúng tôi biết điều này từ những nghiên cứu khác. Chỉ cần mất một phút hít thở chất polyurethane là có thể bắt đầu khó thở rồi”.(...)
Giải pháp đem lại hiệu quả lớn nhất hiện nay là cắt giảm lượng sản phẩm nhựa dùng một lần. “Không có gì vô nghĩa hơn việc tạo ra những thứ tồn tại cả 500 năm nhưng lại chỉ sử dụng trong vòng hai mươi phút”, Galloway nói. “Đó hoàn toàn là cách sử dụng thiếu bền vững”.
(Nguồn: Anh Vũ tổng hợp, Thời báo Tài chính, Bộ Tài chính Việt Nam, đăng ngày 04/01/2023)
Câu 132
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 133
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 134
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 135
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 136
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 137
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 61 đến 65:
(1) Đại dịch đã chỉ ra rằng cách mạng công nghệ đang tiến xa hơn những gì chúng ta có thể nghĩ nhưng cuộc sống số cũng có thể cảm thấy chật chội, một mô phỏng tồi tệ của thế giới thực. Đối với nhiều người, những thay đổi này sẽ rất đáng sợ. Một số công việc sẽ mất đi, nhưng năng suất tổng thể sẽ tăng lên, tạo ra nhiều của cải hơn làm lợi cho tất cả mọi người. Chất lượng cuộc sống con người sẽ được cải thiện. Có những lo ngại về quyền riêng tư, xử lí dữ liệu và vai trò của chính phủ trong việc quản lí các công ty và quản lí chính mình trong lĩnh vực này. Nhưng đấy không phải là những vấn đề không thể giải quyết; chúng ta có thể hưởng lợi ích của cuộc sống số và vẫn có thể bảo vệ quyền riêng tư của chúng ta. Và nếu chúng ta quan tâm phát triển những quy định xung quanh các cuộc cách mạng về AI và kĩ thuật y sinh, chúng ta sẽ không đánh mất những phẩm chất chỉ có ở con người. Thật ra, chúng ta sẽ càng đề cao con người.
(2) Con người lo lắng rằng khi AI trở nên phát triển hơn, chúng ta sẽ dựa vào máy tính của mình nhiều đến mức cuối cùng sẽ coi chúng là bạn và không thể hoạt động nếu không có chúng. Nhưng chuyện đã như vậy rồi mà, điện thoại của tôi có thể cung cấp cho tôi nhiều thông tin hơn bất kì con người nào tôi biết. Nó có thể giải quyết các nhiệm vụ phức tạp trong một nano giây. Nó có thể giúp tôi giải trí với nội dung xuyên thời gian và không gian. Vậy nhưng tôi chưa bao giờ nhầm nó là bạn. Máy tính càng thông minh hơn trong việc tính toán dữ liệu và đưa ra câu trả lời, thì nó càng buộc chúng ta phải suy nghĩ xem cái gì chỉ có ở con người chúng ta, ngoài khả năng suy luận. Thực ra, những cỗ máy thông minh sẽ khiến chúng ta đánh giá cao bạn đồng hành con người nhiều hơn, vì sự sáng tạo, hay thay đổi, không thể đoán trước, ấm áp và gần gũi của họ. Suy nghĩ này không có gì kì lạ. Trong phần lớn lịch sử, con người được ca ngợi vì nhiều phẩm chất khác ngoài khả năng tính toán – dũng cảm, trung thành, độ lượng, đức tin, tình yêu thương. Chuyển đến cuộc sống kĩ thuật số là sâu rộng, nhanh chóng và là hiện thực. Nhưng có lẽ một trong những hệ quả sâu xa nhất của nó sẽ là khiến chúng ta phải trân trọng những điều con người nhất trong ta.”
(Fareed Zakaria, Mười bài học cho thế giới hậu đại dịch, NXB trẻ, 2021, tr. 127)
Câu 138
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 139
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 140
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 141
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 142
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
Ôi quê hương xanh biếc bóng dừa
Có ngờ đâu hôm nay ta trở lại
Quê hương ta tất cả vẫn còn đây
Dù người thân đã ngã xuống đất này
Ta gặp lại những mặt người ta yêu biết mấy
Ta nhìn, ta ngắm, ta say
Ta run run nắm những bàn tay
Thương nhớ dồn trong tay ta nóng bỏng
Đây rồi đoạn đường xưa
Nơi ta vẫn thường đi trong mộng
Kẽo kẹt nhà ai tiếng võng đưa
Ầu ơ…thương nhớ lắm!
Ơi những bông trang trắng, những bông trang hồng
Như tấm lòng em trong trắng thủy chung
Như trái tim em đẹp màu đỏ thắm
Con sông nhỏ tuổi thơ ta đã tắm
Vẫn còn đây nước chẳng đổi dòng
Hoa lục bình tím cả bờ sông.
(“Trở về quê nội” – Lê Anh Xuân)
Câu 143
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 144
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 145
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 146
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 147
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Dựa vào các thông tin sau đây để trả lời các câu hỏi từ câu 108 đến câu 110:
"Sau những năm bôn Ba hầu khắp các châu lục trên thế giới, cuối năm 1917 Nguyễn Tất Thành trở lại Pháp, gia nhập Đảng Xã hội Pháp (1919).
Ngày 18-6-1919, thay mặt những người Việt Nam yêu nước tại Pháp, Nguyễn Tất Thành với tên gọi mới là Nguyễn Ái Quốc gứi đến Hội nghị Vécxai bản Yêu sách của nhân dân An Nam, đòi Chính phủ Pháp và các nước đồng minh thừa nhận các quyền tự do, dân chủ, quyền bình đẳng và quyền tự quyết của dân tộc Việt Nam. Bản yêu sách không được chấp nhận. Vì vậy, "muốn được giải phóng, các dân tộc chỉ có thể trông cậy vào lực lượng của bản thân mình".
Giữa năm 1920, Nguyễn Ái Quốc đọc bản Sơ thảo lần thứ nhất những luận cương về vấn đề dân tộc và vấn đề thuộc địa của V. I. Lênin đăng trên báo Nhân đạo của Đảng Xã hội Pháp. Luận cương của Lênin đã giúp Nguyễn Ái Quốc khẳng định con đường giành độc lập và tự do của nhân dân Việt Nam.
Ngày 25-12-1920, Nguyễn Ái Quốc tham dự Đại hội đại biểu toàn quốc lần thứ XVIII của Đảng Xã hội Pháp họp tại thành phố Tua. Người đã đứng về phía đa số đại biểu Đại hội bỏ phiếu tán thành việc gia nhập thành lập Đảng Cộng sản Pháp. Nguyển Ái Quốc trở thành đảng viên cộng sản và là một trong những người tham gia sáng lập Đảng Cộng sản Pháp".
(Nguồn: SGK Lịch sử 12, NXB Giáo dục Việt Nam, 2023, trang 81-82)
Câu 148
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 149
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 150
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

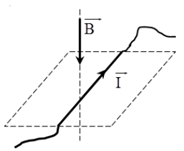
![Một khung dây dẫn tròn, cứng, đặt trong từ trường \[\vec B\] giảm dần đều như hình vẽ. Dòng điện cảm ứng trong khung có chiều (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid3-1721807393.png)
![Âm thanh từ một cái loa đặt phía trên một ống gây ra hiện tượng cộng hưởng của không khí trong ống. Một sóng dừng được hình thành với hai nút và hai bụng như hình vẽ. Tốc độ âm thanh trong không khí là \[340m.{s^{ - 1}}\]. Tần số của âm gần nhất với giá trị nào? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid4-1721807535.png)
![Một mạch dao động LC lí tưởng với q là điện tích trên tụ, i là dòng điện tức thời trong mạch. Đồ thị thể hiện sự phụ thuộc của \[{q^2}\] vào \[{i^2}\] như hình vẽ. Bước sóng mà mạch thu được trong không khí là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid5-1721807668.png)