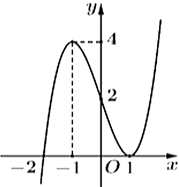
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}.\) Đồ thị \(y = f\left( x \right)\) như hình vẽ. Số đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} + x - 2}}{{{f^2}\left( x \right) - f\left( x \right)}}\) là
A. 4.
B. 3.
Quảng cáo
Trả lời:
Xét hàm số \(y = \frac{{{x^2} + x - 2}}{{{f^2}\left( x \right) - f\left( x \right)}} = \frac{{\left( {x - 1} \right)\left( {x + 2} \right)}}{{f\left( x \right)\left[ {f\left( x \right) - 1} \right]}}\).
Xét phương trình \(f\left( x \right)\left[ {f\left( x \right) - 1} \right] = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f\left( x \right) = 0}\\{f\left( x \right) = 1}\end{array}} \right.\)
• Với \(f\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1\,\,\,({\rm{kep}})}\\{x = - 2\,\,({\rm{don}})}\end{array} \Rightarrow x = 1} \right.\) là tiệm cận đứng, \(x = - 2\) không là tiệm cận đứng.
• Với \[f\left( x \right) = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = {x_1} \in \left( {0\,;\,\,1} \right)}\\{x = {x_2} \in \left( { - 2\,;\,\, - 1} \right)}\end{array} \Rightarrow x = 0\,,\,\,x = {x_1},x = {x_2}} \right.\] đều là các đường tiệm cận đứng.
Vậy đồ thị hàm số có 4 đường TCĐ. Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
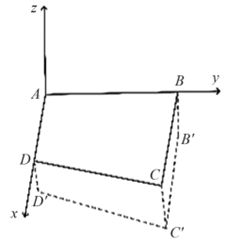
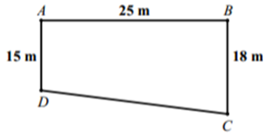
Chọn hệ trục toạ độ \[Oxyz\] sao cho \(O \equiv A\), tia \(Ox \equiv AD\), tia \(Oy \equiv AB.\)
Khi đó, \[A\left( {0\,;\,\,0\,;\,\,0} \right)\,;\,\,B\left( {0\,;\,\,2\,\,500\,;\,\,0} \right)\,;\,\]\[\,C\left( {1\,\,800\,;\,\,2500\,;\,\,0} \right)\,;\]\[D\left( {1500\,\,;\,\,0\,;\,\,0} \right).\]
Khi hạ độ cao các điểm ở các điểm xuống \[B,\,\,C,\,\,D\] thấp hơn so với độ cao ở \(A\) là \[10\,\,{\rm{cm}},\,\,a\,\,{\rm{cm}},\,\,6\,\,{\rm{cm}}\] tương ứng ta có các điểm mới \[B'\left( {0\,;\,\,2\,\,500\,;\,\, - 10} \right)\,;\,\,C'\left( {1800\,;\,\,2500\,;\,\, - a} \right)\,;\,\,\]\[D'\left( {1500\,;\,\,0\,;\,\, - 6} \right).\]Theo bài ra có \(A,\,\,B',\,\,C',\,\,D'\) đồng phẳng.
Phương trình mặt phẳng \(\left( {AB'D'} \right):x + y + 250z = 0.\)
Do \[C'\left( {1\,\,800\,;\,\,2500\,;\,\, - a} \right) \in \left( {AB'D'} \right)\] nên có \(1800 + 2500 - 250a = 0 \Rightarrow a = 17,2.\)
Vậy \(a = 17,2\;\,{\rm{cm}}.\)Chọn B.
Câu 2
Lời giải
Huyết áp giảm nhiều nhất thì hàm số \(G\left( x \right)\) đạt giá trị nhỏ nhất.
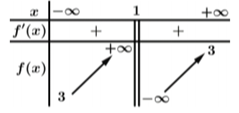
Xét hàm số \(h\left( x \right) = {x^2}\left( {15 - x} \right)\) trên \[\left( {0\,;\,\,15} \right)\], có \[h'\left( x \right) = 30x - 3{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 10}\end{array}} \right.\].
Dựa vào BBT của \(h\left( x \right)\), ta thấy \(h\left( x \right)\) đạt giá trị nhỏ nhất khi \(x = 10.\) Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left( {1\,;\,\,2} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.