Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
Ôi quê hương xanh biếc bóng dừa
Có ngờ đâu hôm nay ta trở lại
Quê hương ta tất cả vẫn còn đây
Dù người thân đã ngã xuống đất này
Ta gặp lại những mặt người ta yêu biết mấy
Ta nhìn, ta ngắm, ta say
Ta run run nắm những bàn tay
Thương nhớ dồn trong tay ta nóng bỏng
Đây rồi đoạn đường xưa
Nơi ta vẫn thường đi trong mộng
Kẽo kẹt nhà ai tiếng võng đưa
Ầu ơ…thương nhớ lắm!
Ơi những bông trang trắng, những bông trang hồng
Như tấm lòng em trong trắng thủy chung
Như trái tim em đẹp màu đỏ thắm
Con sông nhỏ tuổi thơ ta đã tắm
Vẫn còn đây nước chẳng đổi dòng
Hoa lục bình tím cả bờ sông.
(“Trở về quê nội” – Lê Anh Xuân)
Hai dòng thơ đầu có sử dụng những thành phần biệt lập nào?
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
Ôi quê hương xanh biếc bóng dừa
Có ngờ đâu hôm nay ta trở lại
Quê hương ta tất cả vẫn còn đây
Dù người thân đã ngã xuống đất này
Ta gặp lại những mặt người ta yêu biết mấy
Ta nhìn, ta ngắm, ta say
Ta run run nắm những bàn tay
Thương nhớ dồn trong tay ta nóng bỏng
Đây rồi đoạn đường xưa
Nơi ta vẫn thường đi trong mộng
Kẽo kẹt nhà ai tiếng võng đưa
Ầu ơ…thương nhớ lắm!
Ơi những bông trang trắng, những bông trang hồng
Như tấm lòng em trong trắng thủy chung
Như trái tim em đẹp màu đỏ thắm
Con sông nhỏ tuổi thơ ta đã tắm
Vẫn còn đây nước chẳng đổi dòng
Hoa lục bình tím cả bờ sông.
(“Trở về quê nội” – Lê Anh Xuân)
Quảng cáo
Trả lời:
Hai dòng thơ đầu có sử dụng các thành phần biệt lập: Thành phần cảm thán: “Ôi”. Thành phần tình thái: “Có ngờ đâu”. Chọn B.
Câu hỏi cùng đoạn
Câu 2:
Hai dòng thơ đầu đã diễn tả tâm trạng gì của nhà thơ?
Hai dòng thơ đầu thể hiện tâm trạng xúc động rưng rưng của nhà thơ khi trở về quê cũ. Chọn D.
Câu 3:
Những hình ảnh nào trong đoạn thơ đã thể hiện được vẻ đẹp và sức sống tiềm tàng, mãnh liệt của quê hương?
Những hình ảnh trong đoạn thơ đã thể hiện được vẻ đẹp và sức sống tiềm tàng, mãnh liệt của quê hương: xanh biếc bóng dừa, những mặt người ta yêu biết mấy, đoạn đường xưa, tiếng võng đưa, những bông trang trắng, những bông trang hồng, con sông nước chẳng đổi dòng, hoa lục bình tím cả bờ sông. Chọn A.
Câu 4:
Chữ “tím” trong câu thơ “Hoa lục bình tím cả bờ sông” có sự chuyển đổi từ loại như thế nào?
Trong câu thơ “Hoa lục bình tím cả bờ sông”, chữ “tím” ở đây có sự chuyển đổi từ loại từ tính từ sang động từ (tím: nhuộm tím cả bờ sông). Chọn A.
Câu 5:
Điệp từ “ta” được điệp lại nhiều lần kết hợp với một loạt những động từ “gặp lại”, “yêu”, “nhìn”, “say”, “ngắm”,… có tác dụng nhấn mạnh điều gì?
Điệp từ “ta” được điệp lại nhiều lần kết hợp với một loạt những động từ “gặp lại”, “yêu”, “nhìn”, “say”, “ngắm”,… nhằm thể hiện tình yêu quê hương tha thiết và nỗi xúc động, bồi hồi của tác giả khi trở lại quê nhà sau bao năm năm xa cách. Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
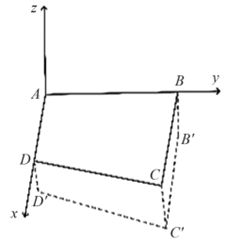
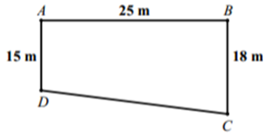
Chọn hệ trục toạ độ \[Oxyz\] sao cho \(O \equiv A\), tia \(Ox \equiv AD\), tia \(Oy \equiv AB.\)
Khi đó, \[A\left( {0\,;\,\,0\,;\,\,0} \right)\,;\,\,B\left( {0\,;\,\,2\,\,500\,;\,\,0} \right)\,;\,\]\[\,C\left( {1\,\,800\,;\,\,2500\,;\,\,0} \right)\,;\]\[D\left( {1500\,\,;\,\,0\,;\,\,0} \right).\]
Khi hạ độ cao các điểm ở các điểm xuống \[B,\,\,C,\,\,D\] thấp hơn so với độ cao ở \(A\) là \[10\,\,{\rm{cm}},\,\,a\,\,{\rm{cm}},\,\,6\,\,{\rm{cm}}\] tương ứng ta có các điểm mới \[B'\left( {0\,;\,\,2\,\,500\,;\,\, - 10} \right)\,;\,\,C'\left( {1800\,;\,\,2500\,;\,\, - a} \right)\,;\,\,\]\[D'\left( {1500\,;\,\,0\,;\,\, - 6} \right).\]Theo bài ra có \(A,\,\,B',\,\,C',\,\,D'\) đồng phẳng.
Phương trình mặt phẳng \(\left( {AB'D'} \right):x + y + 250z = 0.\)
Do \[C'\left( {1\,\,800\,;\,\,2500\,;\,\, - a} \right) \in \left( {AB'D'} \right)\] nên có \(1800 + 2500 - 250a = 0 \Rightarrow a = 17,2.\)
Vậy \(a = 17,2\;\,{\rm{cm}}.\)Chọn B.
Câu 2
Lời giải
Huyết áp giảm nhiều nhất thì hàm số \(G\left( x \right)\) đạt giá trị nhỏ nhất.
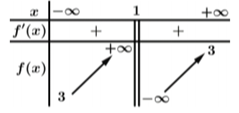
Xét hàm số \(h\left( x \right) = {x^2}\left( {15 - x} \right)\) trên \[\left( {0\,;\,\,15} \right)\], có \[h'\left( x \right) = 30x - 3{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 10}\end{array}} \right.\].
Dựa vào BBT của \(h\left( x \right)\), ta thấy \(h\left( x \right)\) đạt giá trị nhỏ nhất khi \(x = 10.\) Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left( {1\,;\,\,2} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.