Trong tập hợp các số phức cho phương trình \({z^3} + \left( {1 - 2m} \right){z^2} + 2mz + 4m = 0\) với tham số \(m \in \mathbb{R}.\) Gọi \(S\) là tập hợp các giá trị của \(m\) để phương trình có 3 nghiệm phân biệt và 3 điểm biểu diễn 3 nghiệm đó tạo thành tam giác đều. Tổng tất cả các phần tử của tập \(S\) bằng
Trong tập hợp các số phức cho phương trình \({z^3} + \left( {1 - 2m} \right){z^2} + 2mz + 4m = 0\) với tham số \(m \in \mathbb{R}.\) Gọi \(S\) là tập hợp các giá trị của \(m\) để phương trình có 3 nghiệm phân biệt và 3 điểm biểu diễn 3 nghiệm đó tạo thành tam giác đều. Tổng tất cả các phần tử của tập \(S\) bằng
Quảng cáo
Trả lời:
Ta có \[{z^3} + \left( {1 - 2m} \right){z^2} + 2mz + 4m = 0 \Leftrightarrow \left( {z + 1} \right)\left( {{z^2} - 2mz + 4m} \right) = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{z = - 1}\\{{z^2} - 2mz + 4m = 0}\end{array}} \right.\)
Yêu cầu bài toán \( \Leftrightarrow (1)\) có hai nghiệm phức phân biệt (phần ảo khác 0\(){z_1},{z_2}\) thoả mãn:
\(\left| {{z_1} + 1} \right| = \left| {{z_1} - {z_2}} \right| \Leftrightarrow {\left| {{z_1} + 1} \right|^2} = {\left| {{z_1} - {z_2}} \right|^2}{m^2} - 4m < 0\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left( {{z_1} + 1} \right)\left( {\overline {{z_1}} + 1} \right) = 4{z_1}{z_2} - {{\left( {{z_1} + {z_2}} \right)}^2}}\\{0 < m < 4}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left( {{z_1} + 1} \right)\left( {{z_2} + 1} \right) = 4{z_1}{z_2} - {{\left( {{z_1} + {z_2}} \right)}^2}}\\{0 < m < 4}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{z_1} + {z_2} + 1 = 3{z_1}{z_2} - {{\left( {{z_1} + {z_2}} \right)}^2}}\\{0 < m < 4}\end{array}} \right.\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{2m + 1 = 12m - 4{m^2}}\\{0 < m < 4}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4{m^2} - 10m + 1 = 0}\\{0 < m < 4}\end{array}} \right. \Leftrightarrow m = \frac{{5 \pm \sqrt {21} }}{4}.\)
Vậy tổng tất cả các phần tử của tập \(S\) bằng \(\frac{5}{2}.\)
Đáp án: \(\frac{5}{2}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
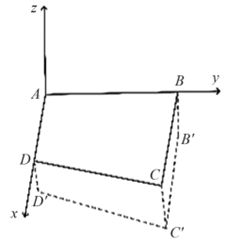
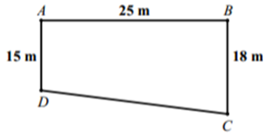
Chọn hệ trục toạ độ \[Oxyz\] sao cho \(O \equiv A\), tia \(Ox \equiv AD\), tia \(Oy \equiv AB.\)
Khi đó, \[A\left( {0\,;\,\,0\,;\,\,0} \right)\,;\,\,B\left( {0\,;\,\,2\,\,500\,;\,\,0} \right)\,;\,\]\[\,C\left( {1\,\,800\,;\,\,2500\,;\,\,0} \right)\,;\]\[D\left( {1500\,\,;\,\,0\,;\,\,0} \right).\]
Khi hạ độ cao các điểm ở các điểm xuống \[B,\,\,C,\,\,D\] thấp hơn so với độ cao ở \(A\) là \[10\,\,{\rm{cm}},\,\,a\,\,{\rm{cm}},\,\,6\,\,{\rm{cm}}\] tương ứng ta có các điểm mới \[B'\left( {0\,;\,\,2\,\,500\,;\,\, - 10} \right)\,;\,\,C'\left( {1800\,;\,\,2500\,;\,\, - a} \right)\,;\,\,\]\[D'\left( {1500\,;\,\,0\,;\,\, - 6} \right).\]Theo bài ra có \(A,\,\,B',\,\,C',\,\,D'\) đồng phẳng.
Phương trình mặt phẳng \(\left( {AB'D'} \right):x + y + 250z = 0.\)
Do \[C'\left( {1\,\,800\,;\,\,2500\,;\,\, - a} \right) \in \left( {AB'D'} \right)\] nên có \(1800 + 2500 - 250a = 0 \Rightarrow a = 17,2.\)
Vậy \(a = 17,2\;\,{\rm{cm}}.\)Chọn B.
Câu 2
Lời giải
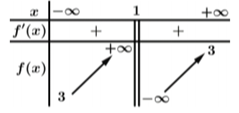
Huyết áp giảm nhiều nhất thì hàm số \(G\left( x \right)\) đạt giá trị nhỏ nhất.
Xét hàm số \(h\left( x \right) = {x^2}\left( {15 - x} \right)\) trên \[\left( {0\,;\,\,15} \right)\], có \[h'\left( x \right) = 30x - 3{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 10}\end{array}} \right.\].
Dựa vào BBT của \(h\left( x \right)\), ta thấy \(h\left( x \right)\) đạt giá trị nhỏ nhất khi \(x = 10.\) Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left( {1\,;\,\,2} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.