Đọc đoạn trích sau và trả lời câu hỏi:
Xuân đương tới, nghĩa là xuân đương qua,
Xuân còn non, nghĩa là xuân sẽ già,
Mà xuân hết, nghĩa là tôi cũng mất.
Lòng tôi rộng, nhưng lượng trời cứ chật,
Không cho dài thời trẻ của nhân gian,
Nói làm chi rằng xuân vẫn tuần hoàn,
Nếu tuổi trẻ chẳng hai lần thắm lại!
(Vội vàng – Xuân Diệu)
Chủ đề nổi bật bao trùm đoạn thơ là gì?
Đọc đoạn trích sau và trả lời câu hỏi:
Xuân đương tới, nghĩa là xuân đương qua,
Xuân còn non, nghĩa là xuân sẽ già,
Mà xuân hết, nghĩa là tôi cũng mất.
Lòng tôi rộng, nhưng lượng trời cứ chật,
Không cho dài thời trẻ của nhân gian,
Nói làm chi rằng xuân vẫn tuần hoàn,
Nếu tuổi trẻ chẳng hai lần thắm lại!
(Vội vàng – Xuân Diệu)
Chủ đề nổi bật bao trùm đoạn thơ là gì?
Quảng cáo
Trả lời:
Từ xa xưa thi sĩ đã từng than thở về sự ngắn ngủi của kiếp người, người ta gọi là kiếp phù vân hay bóng câu qua cửa sổ. Nhưng con người thời trung đại hình như yên trí bình tĩnh với quan niệm thời gian tuần hoàn với chu kì bốn mùa, cũng như chu kì 3 vạn 6 ngàn ngày của kiếp người. Họ cho rằng, người chết chưa hẳn là hư vô, có thể cùng trời đất tuần hoàn trở lại, hết một vòng, thời gian lại quay về điểm xuất phát ban đầu (Quan niệm về trời đất và con người nhất thể). Còn con người hiện đại sống bằng quan niệm thời gian tuyến tính. Thời gian như một dòng chảy vô thủy vô chung mà mỗi một khoảnh khắc đi qua là mất đi vĩnh viễn. Niềm tin xưa đã mất ở các nhà thơ khi ý thức cá nhân thức tỉnh. Thước đo thời gian của thi sĩ là tuổi trẻ. Tuổi trẻ đã một đi không trở lại thì làm chi có sự tuần hoàn. Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
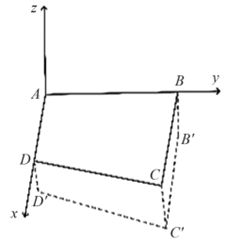
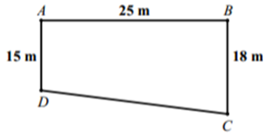
Chọn hệ trục toạ độ \[Oxyz\] sao cho \(O \equiv A\), tia \(Ox \equiv AD\), tia \(Oy \equiv AB.\)
Khi đó, \[A\left( {0\,;\,\,0\,;\,\,0} \right)\,;\,\,B\left( {0\,;\,\,2\,\,500\,;\,\,0} \right)\,;\,\]\[\,C\left( {1\,\,800\,;\,\,2500\,;\,\,0} \right)\,;\]\[D\left( {1500\,\,;\,\,0\,;\,\,0} \right).\]
Khi hạ độ cao các điểm ở các điểm xuống \[B,\,\,C,\,\,D\] thấp hơn so với độ cao ở \(A\) là \[10\,\,{\rm{cm}},\,\,a\,\,{\rm{cm}},\,\,6\,\,{\rm{cm}}\] tương ứng ta có các điểm mới \[B'\left( {0\,;\,\,2\,\,500\,;\,\, - 10} \right)\,;\,\,C'\left( {1800\,;\,\,2500\,;\,\, - a} \right)\,;\,\,\]\[D'\left( {1500\,;\,\,0\,;\,\, - 6} \right).\]Theo bài ra có \(A,\,\,B',\,\,C',\,\,D'\) đồng phẳng.
Phương trình mặt phẳng \(\left( {AB'D'} \right):x + y + 250z = 0.\)
Do \[C'\left( {1\,\,800\,;\,\,2500\,;\,\, - a} \right) \in \left( {AB'D'} \right)\] nên có \(1800 + 2500 - 250a = 0 \Rightarrow a = 17,2.\)
Vậy \(a = 17,2\;\,{\rm{cm}}.\)Chọn B.
Câu 2
Lời giải
Huyết áp giảm nhiều nhất thì hàm số \(G\left( x \right)\) đạt giá trị nhỏ nhất.
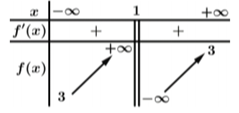
Xét hàm số \(h\left( x \right) = {x^2}\left( {15 - x} \right)\) trên \[\left( {0\,;\,\,15} \right)\], có \[h'\left( x \right) = 30x - 3{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 10}\end{array}} \right.\].
Dựa vào BBT của \(h\left( x \right)\), ta thấy \(h\left( x \right)\) đạt giá trị nhỏ nhất khi \(x = 10.\) Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left( {1\,;\,\,2} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.