Cho \((H)\) là đa giác đều \[2n\] đỉnh nội tiếp đường tròn tâm \(O\,\,(n \in \mathbb{N},\,\,n > 2).\) Gọi \(S\) là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác \((H).\) Chọn ngẫu nhiên một tam giác thuộc tập \(S,\) biết rằng xác suất chọn một tam giác vuông trong tập \(S\) là \(\frac{3}{{29}}\). Tìm \(n\).
Cho \((H)\) là đa giác đều \[2n\] đỉnh nội tiếp đường tròn tâm \(O\,\,(n \in \mathbb{N},\,\,n > 2).\) Gọi \(S\) là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác \((H).\) Chọn ngẫu nhiên một tam giác thuộc tập \(S,\) biết rằng xác suất chọn một tam giác vuông trong tập \(S\) là \(\frac{3}{{29}}\). Tìm \(n\).
Quảng cáo
Trả lời:
Số phần tử của không gian mẫu \(n\left( \Omega \right) = C_{2n}^3.\)
Tam giác vuông được chọn là tam giác chứa cạnh là đường kính của đường tròn tâm \[O.\]
Đa giác đều 2n đỉnh chứa 2n đường chéo là đường kính của đường tròn tâm \[O,\] mỗi đường kính tạo nên \(2n - 2\) tam giác vuông.
Do đó số tam giác vuông trong tập \[S\] là: \(\frac{{2n}}{2} \cdot \left( {2n - 2} \right) = 2n\left( {n - 1} \right).\)
Xác suất chọn một tam giác vuông trong tập \[S\] là:
\(\frac{{2n\left( {n - 1} \right)}}{{C_{2n}^3}} = \frac{{2n\left( {n - 1} \right)}}{{\frac{{\left( {2n} \right)!}}{{\left( {2n - 3} \right)!.3!}}}} = \frac{{2n\left( {n - 1} \right)}}{{\frac{{2n\left( {2n - 1} \right)\left( {2n - 2} \right)}}{6}}}\)\( = \frac{3}{{2n - 1}} = \frac{3}{{29}} \Rightarrow n = 15\).
Đáp án: 15.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
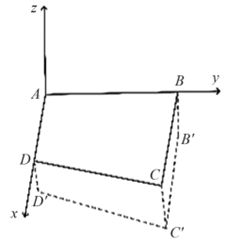
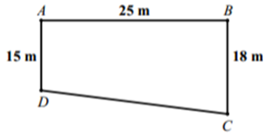
Chọn hệ trục toạ độ \[Oxyz\] sao cho \(O \equiv A\), tia \(Ox \equiv AD\), tia \(Oy \equiv AB.\)
Khi đó, \[A\left( {0\,;\,\,0\,;\,\,0} \right)\,;\,\,B\left( {0\,;\,\,2\,\,500\,;\,\,0} \right)\,;\,\]\[\,C\left( {1\,\,800\,;\,\,2500\,;\,\,0} \right)\,;\]\[D\left( {1500\,\,;\,\,0\,;\,\,0} \right).\]
Khi hạ độ cao các điểm ở các điểm xuống \[B,\,\,C,\,\,D\] thấp hơn so với độ cao ở \(A\) là \[10\,\,{\rm{cm}},\,\,a\,\,{\rm{cm}},\,\,6\,\,{\rm{cm}}\] tương ứng ta có các điểm mới \[B'\left( {0\,;\,\,2\,\,500\,;\,\, - 10} \right)\,;\,\,C'\left( {1800\,;\,\,2500\,;\,\, - a} \right)\,;\,\,\]\[D'\left( {1500\,;\,\,0\,;\,\, - 6} \right).\]Theo bài ra có \(A,\,\,B',\,\,C',\,\,D'\) đồng phẳng.
Phương trình mặt phẳng \(\left( {AB'D'} \right):x + y + 250z = 0.\)
Do \[C'\left( {1\,\,800\,;\,\,2500\,;\,\, - a} \right) \in \left( {AB'D'} \right)\] nên có \(1800 + 2500 - 250a = 0 \Rightarrow a = 17,2.\)
Vậy \(a = 17,2\;\,{\rm{cm}}.\)Chọn B.
Câu 2
Lời giải
Huyết áp giảm nhiều nhất thì hàm số \(G\left( x \right)\) đạt giá trị nhỏ nhất.
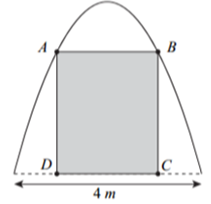
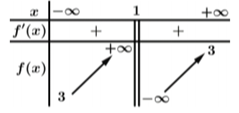
Xét hàm số \(h\left( x \right) = {x^2}\left( {15 - x} \right)\) trên \[\left( {0\,;\,\,15} \right)\], có \[h'\left( x \right) = 30x - 3{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 10}\end{array}} \right.\].
Dựa vào BBT của \(h\left( x \right)\), ta thấy \(h\left( x \right)\) đạt giá trị nhỏ nhất khi \(x = 10.\) Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left( {1\,;\,\,2} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.