Gọi \(m\) là tham số thực để giá trị lớn nhất của hàm số \(y = \left| {{x^2} + 2x + m - 4} \right|\) trên đoạn \(\left[ { - 2;1} \right]\) đạt giá trị nhỏ nhất. Giá trị của \(m\) là
A.1.
B.3.
C.5.
D.4.
Quảng cáo
Trả lời:
Đáp án B.
Xét hàm số \(f\left( x \right) = {x^2} + 2x + m - 4\) trên đoạn \(\left[ { - 2;1} \right].\)
Ta có: \(f'\left( x \right) = 2x + 2 = 0 \Leftrightarrow 2x = - 2 \Leftrightarrow x = - 1\)
\(y\left( { - 2} \right) = \left| {m - 4} \right|;y\left( { - 1} \right) = \left| {m - 5} \right|;y\left( 1 \right) = \left| {m - 1} \right|\)
Với \(\forall m\) ta luôn có: \(m - 1 >m - 4 >m - 5\) nên \(\mathop {Max}\limits_{\left[ { - 2;1} \right]} y = Max\left\{ {\left| {m - 1} \right|;\left| {m - 5} \right|} \right\}\)
Mà \(\left| {m - 1} \right| \ge \left| {m - 5} \right| \Leftrightarrow {\left( {m - 1} \right)^2} \ge {\left( {m - 5} \right)^2} \Leftrightarrow {m^2} - 2m + 1 \ge {m^2} - 10m + 25 \Leftrightarrow 8m \ge 24 \Leftrightarrow m \ge 3\)
Do đó: \(\mathop {Max}\limits_{\left[ { - 2;1} \right]} y = Max\left\{ {\left| {m - 1} \right|;\left| {m - 5} \right|} \right\} = \left\{ \begin{array}{l}\left| {m - 1} \right|{\rm{ }}khi{\rm{ }}m \ge 3\\\left| {m - 5} \right|{\rm{ }}khi{\rm{ }}m \le 3\end{array} \right.\)
Xét hàm số \(g\left( m \right) = \left\{ \begin{array}{l}\left| {m - 1} \right|{\rm{ }}khi{\rm{ }}m \ge 3\\\left| {m - 5} \right|{\rm{ }}khi{\rm{ }}m \le 3\end{array} \right. \Rightarrow g\left( m \right) = \left\{ \begin{array}{l}m - 1{\rm{ }}khi{\rm{ }}m \ge 3\\5 - m{\rm{ }}khi{\rm{ }}m \le 3\end{array} \right.\)
Đồ thị hàm số như sau:
![Gọi m là tham số thực để giá trị lớn nhất của hàm số y = |x^2 + 2x + m - 4| trên đoạn [-2;1] đạt giá trị nhỏ nhất. Giá trị của m là (ảnh 1)](https://video.vietjack.com/upload2/images/1651250052/1651250242-image12.png)
Từ đồ thị ta thấy \(Min\left[ {g\left( m \right)} \right] = 2\) khi \(m = 3\)
Vậy khi \(m = 3\) thì giá trị lớn nhất của hàm số \(y = \left| {{x^2} + 2x + m - 4} \right|\) trên đoạn \(\left[ { - 2;1} \right]\) đạt giá trị
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\(1,50{m^3}.\)
B.\(1,33{m^3}.\)
C.\(1,61{m^3}.\)
D. \(0,73{m^3}.\)
Lời giải
Đáp án D.
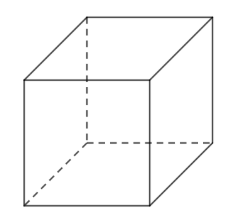
Gọi \(x,2x,h\) lần lượt là ba kích thước của hồ. \(\left( {x \ge 0} \right)\)
Diện tích xung quanh và đáy hồ: \(S = 2{x^2} + 2.xh + 2.2xh = 2{x^2} + 6xh = 4\)
\( \Rightarrow h = \frac{{2 - {x^2}}}{{3x}}\left( {0 \le x \le \sqrt 2 } \right).\)
Thể tích hồ \(V = x.2x.h = \frac{{2x\left( {2 - {x^2}} \right)}}{3}\)
\(V' = - 2{x^2} + \frac{4}{3}\)
\(V' = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{\sqrt 6 }}{3}\\x = \frac{{ - \sqrt 6 }}{3}\left( l \right)\end{array} \right.\)
\(V\left( 0 \right) = 0\)
\(V\left( {\sqrt 2 } \right) = 0\)
\(V\left( {\frac{{\sqrt 6 }}{3}} \right) = \frac{{8\sqrt 6 }}{{27}} \approx 0.73\)
Vậy thể tích lớn nhất là câu D.
Lời giải
Đáp ánA.
Ta có:
\(\begin{array}{l}y = \frac{{x + 2}}{{x + 3m}}(x \ne - 3m)\\ = >y' = \frac{{3m - 2}}{{{{(x + 3m)}^2}}}\end{array}\)
Để hàm số đồng biến trên \(( - \infty ; - 6) = >y' \ge 0\forall x \in ( - \infty ; - 6)\)
\(\begin{array}{l} < = >\left\{ \begin{array}{l}\frac{{3m - 2}}{{{{(x + 3m)}^2}}} \ge 0\\ - 3m \ge - 6\end{array} \right.\\ < = >\left\{ \begin{array}{l}m \ge \frac{2}{3}\\m \le 2\end{array} \right. = >\frac{2}{3} \le m \le 2\end{array}\)
Với \(m \in (0;20]\) và m nguyên thì ta tìm được 2 giá trị của m thỏa mãn.
Câu 3
A.\(y' = 4{x^3}.\)
B.\(y' = 0.\)
C.\(y' = 4{x^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.0.
B.\( - 16.\)
C.\( - 23.\)
D.4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\(\left( { - \infty ; - \frac{1}{2}} \right).\)
B.\(\left( { - \frac{1}{2}; + \infty } \right).\)
C.\(\left( {0; + \infty } \right).\)
D. \(\left( { - \infty ;0} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
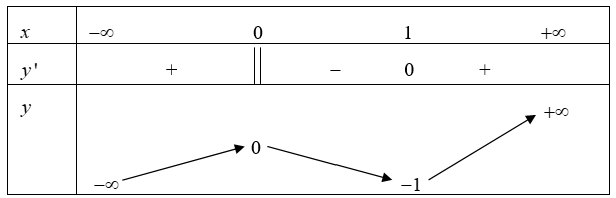
A. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng \( - 1.\)
B. Hàm số có đúng một cực trị.
C. Hàm số có giá trị cực tiểu bằng 1.
D. Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.