Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x - 3} \right)^{2020}}\left( {{\pi ^{2x}} - {\pi ^x} + 2021} \right)\left( {{x^2} - 2x} \right),\forall x \in \mathbb{R}.\) Gọi \(S\) là tập các giá trị nguyên của tham số \(m\) để hàm số \(y = f\left( {{x^2} - 8x + m} \right)\) có đúng ba điểm cực trị \({x_1},{x_2},{x_3}\) thỏa mãn \(x_1^2 + x_2^2 + x_3^2 = 50.\) Khi đó tổng các phần tử của \(S\) bằng
A. 17.
B. 33.
C. 35.
D. 51.
Quảng cáo
Trả lời:
Đáp án D.
Ta có: \(f'\left( x \right) = 0 \Leftrightarrow {\left( {x - 3} \right)^{2020}}\left( {{\pi ^{2x}} - {\pi ^x} + 2021} \right)\left( {{x^2} - 2x} \right) = 0\left( * \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 3\\{\pi ^{2x}} - {\pi ^x} + 2021 = 0\\{x^2} - 2x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 2\\x = 0\end{array} \right.\) (trong đó \(x = 3\) là nghiệm bội chẵn).
Suy ra: \(y' = \left( {2x - 8} \right).f'\left( {{x^2} - 8x + m} \right),y' = 0 \Leftrightarrow \left( {2x - 8} \right).f'\left( {{x^2} - 8x + m} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}2x - 8 = 0\\f'\left( {{x^2} - 8x + m} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\\{x^2} - 8x + m = 3{\rm{ }}\left( 1 \right)\\{x^2} - 8x + m = 2{\rm{ }}\left( 2 \right)\\{x^2} - 8x + m = 0{\rm{ }}\left( 3 \right)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\\{x^2} - 8x = 3 - m{\rm{ }}\left( 1 \right)\\{x^2} - 8x = 2 - m{\rm{ }}\left( 2 \right)\\{x^2} - 8x = - m{\rm{ }}\left( 3 \right)\end{array} \right.\)
Xét hàm số \(y = h\left( x \right) = {x^2} - 8x,h'\left( x \right) = 2x - 8,h'\left( x \right) = 0 \Leftrightarrow 2x - 8 = 0 \Leftrightarrow x = 4.\)
Ta có bảng biến thiên của hàm số \(y = h\left( x \right).\)
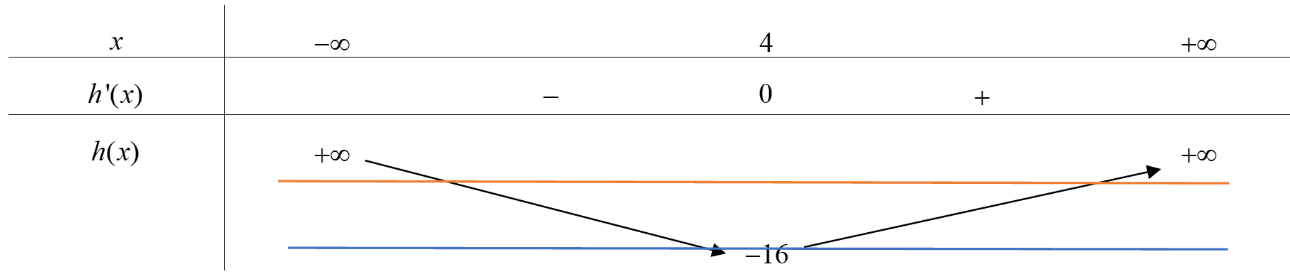
Vì \(x = 3\) là nghiệm bội chẵn của phương trình \(f'\left( x \right) = 0\) nên nghiệm của phương trình \(\left( 1 \right)\) không phải là điểm cực trị của hàm số.
Từ bảng biến thiên suy ra, hàm số có đúng ba điểm cực trị khi phương trình \(\left( 2 \right)\) có hai nghiệm phân biệt đồng thời phương trình \(\left( 3 \right)\) vô nghiệm hoặc có nghiệm duy nhất \(x = 4.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2 - m >- 16\\ - m \le - 16\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 18\\m \ge 16\end{array} \right. \Rightarrow m \in \left\{ {16;17} \right\}\).
Nếu \(x = 4\) là nghiệm của phương trình \(\left( 3 \right)\) thì \(m = 16,\) suy ra phương trình \(\left( 2 \right) \Leftrightarrow {x^2} - 8x + 14 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4 - \sqrt 2 \\x = 4 + \sqrt 2 \end{array} \right.\) (không thỏa mãn \(x_1^2 + x_2^2 + x_3^2 = 50).\)
Nếu \(m = 17\) thì phương trình \(\left( 3 \right)\) vô nghiệm, phương trình \(\left( 2 \right) \Leftrightarrow {x^2} - 8x + 15 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 5\end{array} \right.\) (thỏa mãn: \({3^2} + {4^2} + {5^2} = 50).\)
Vậy \(S = \left\{ {17} \right\}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.\(1,50{m^3}.\)
B.\(1,33{m^3}.\)
C.\(1,61{m^3}.\)
D. \(0,73{m^3}.\)
Lời giải
Đáp án D.
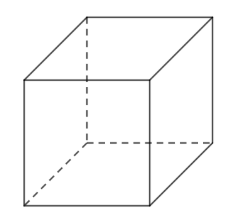
Gọi \(x,2x,h\) lần lượt là ba kích thước của hồ. \(\left( {x \ge 0} \right)\)
Diện tích xung quanh và đáy hồ: \(S = 2{x^2} + 2.xh + 2.2xh = 2{x^2} + 6xh = 4\)
\( \Rightarrow h = \frac{{2 - {x^2}}}{{3x}}\left( {0 \le x \le \sqrt 2 } \right).\)
Thể tích hồ \(V = x.2x.h = \frac{{2x\left( {2 - {x^2}} \right)}}{3}\)
\(V' = - 2{x^2} + \frac{4}{3}\)
\(V' = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{\sqrt 6 }}{3}\\x = \frac{{ - \sqrt 6 }}{3}\left( l \right)\end{array} \right.\)
\(V\left( 0 \right) = 0\)
\(V\left( {\sqrt 2 } \right) = 0\)
\(V\left( {\frac{{\sqrt 6 }}{3}} \right) = \frac{{8\sqrt 6 }}{{27}} \approx 0.73\)
Vậy thể tích lớn nhất là câu D.
Lời giải
Đáp ánA.
Ta có:
\(\begin{array}{l}y = \frac{{x + 2}}{{x + 3m}}(x \ne - 3m)\\ = >y' = \frac{{3m - 2}}{{{{(x + 3m)}^2}}}\end{array}\)
Để hàm số đồng biến trên \(( - \infty ; - 6) = >y' \ge 0\forall x \in ( - \infty ; - 6)\)
\(\begin{array}{l} < = >\left\{ \begin{array}{l}\frac{{3m - 2}}{{{{(x + 3m)}^2}}} \ge 0\\ - 3m \ge - 6\end{array} \right.\\ < = >\left\{ \begin{array}{l}m \ge \frac{2}{3}\\m \le 2\end{array} \right. = >\frac{2}{3} \le m \le 2\end{array}\)
Với \(m \in (0;20]\) và m nguyên thì ta tìm được 2 giá trị của m thỏa mãn.
Câu 3
A.\(y' = 4{x^3}.\)
B.\(y' = 0.\)
C.\(y' = 4{x^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.0.
B.\( - 16.\)
C.\( - 23.\)
D.4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\(\left( { - \infty ; - \frac{1}{2}} \right).\)
B.\(\left( { - \frac{1}{2}; + \infty } \right).\)
C.\(\left( {0; + \infty } \right).\)
D. \(\left( { - \infty ;0} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
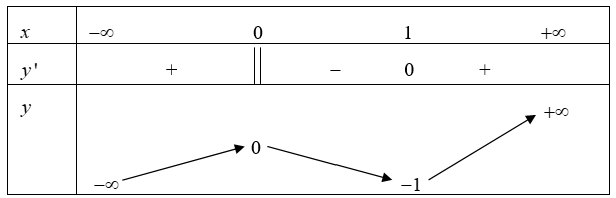
A. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng \( - 1.\)
B. Hàm số có đúng một cực trị.
C. Hàm số có giá trị cực tiểu bằng 1.
D. Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.