Câu hỏi:

06/05/2022 594

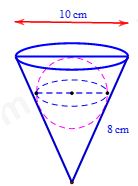
Bạn An có một cốc hình nón có đường kính đáy là 10cm và độ dài đường sinh là 8cm. Bạn dự định đựng một viên bị hình cầu sao cho toàn bộ viên bi nằm trong cốc (không phân nào của viên bị cao hơn miệng cốc). Hỏi bạn An có thể đựng được viên bị có đường kính lớn nhất bằng bao nhiêu?

A. $\frac{32}{\sqrt{39}} cm$

B. $\frac{64}{\sqrt{39}} cm$

C. $\frac{10 \sqrt{39}}{13} cm$

D. $\frac{5 \sqrt{39}}{13} cm$

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá tư duy Đọc hiểu, Toán học - ĐH Bách khoa năm 2023 - 2024 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương pháp giải:

Bước 1: Xét thiết diện qua trục.

Bước 2: Xác định vị trí của viên bi thỏa mãn bài toán

Bước 3: Tính đường kính viên bi

Áp dụng công thức tính bán kính đường tròn nội tiếp $r = \frac{S}{p}$ với $p = \frac{a + b + c}{2}$

Giải chi tiết:

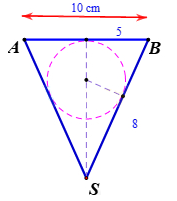
Bạn An có một cốc hình nón có đường kính đáy là 10cm và độ dài đường sinh là 8cm. Bạn dự định đựng một viên bị hình cầu sao (ảnh 2)

Bước 1: Xét thiết diện qua trục.

Thiết diện qua trục là một tam giác cân có cạnh bên là 8cm và cạnh đáy là 10 cm (tam giác SAB)

Bước 2: Xác định vị trí của viên bi thỏa mãn bài toán

Viên bi bị cắt theo chính thiết diện đó thì sẽ tiếp xúc với hai cạnh bên.

Viên bi càng tiến gần đáy thì càng lớn.

Để viên bị có đường kính lớn nhất thì viên bi phải tiếp xúc với mặt trên của cốc nước (miễn là viên bi không cao hơn miệng cốc)

Bước 3: Tính đường kính viên bi

$p = \frac{8 + 8 + 10}{2} = 13$

$\begin{array}{l} r = \frac{S}{p} = \frac{5 \sqrt{8^{2} - 5^{2}}}{13} = \frac{5 \sqrt{39}}{13} \\ d = 2 r = \frac{10 \sqrt{39}}{13} (c m) \end{array}$

Chọn C

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chóp S ABC có SA ^ ( ABC ), tam giác ABC vuông tại B , SA = BC = a , AC = 2 a. Khoảng cách từ điểm A đến mặt phẳng (SBC) là

A. a

B. $\sqrt{2} a$

C. $a \sqrt{3}$

D. $\frac{a \sqrt{3}}{2}$

Lời giải

Phương pháp giải:

Bước 1: Kẻ AH vuông góc với SB. Chứng minh AH⊥(SBC)

Bước 2: Tính AH

Giải chi tiết:

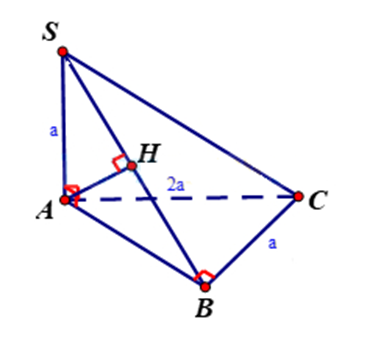
: Cho hình chóp S ABC có SA   ABC , tam giác ABC vuông tại B , SA = BC = a , AC  2 a. Khoảng cách từ điểm A đến mặt phẳng (SBC) (ảnh 1)

Bước 1: Kẻ AH vuông góc với SB. Chứng minh $A H = d (A, (S B C))$

Kẻ AH vuông góc với SB.

Ta có:

$\{\begin{cases} SA ⊥ (A B C) \Rightarrow S A ⊥ B C \\ B C ⊥ A B \end{cases} \Rightarrow B C ⊥ (S A B) = > B C ⊥ A H$

Lại có $A H ⊥ S B = > A H ⊥ (S B C) \Rightarrow A H = d (A, (S B C))$

Bước 2: Tính AH

Xét tam giác vuông ABC có: $A B = \sqrt{A C^{2} - B C^{2}} = a \sqrt{3}$

Xét tam giác vuông SAB có: $\frac{1}{A H^{2}} = \frac{1}{S A^{2}} + \frac{1}{A B^{2}} = \frac{1}{a^{2}} + \frac{1}{3 a^{2}} = \frac{4}{3 a^{2}} = > A H = \frac{a \sqrt{3}}{2}$

Chọn D

Câu 2

Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 lập được bao nhiêu số tự nhiên gồm 3 chữ số đôi một khác nhau và số đó chia hết cho 3.

A. 180

B. 162

C. 210

D. 30

Lời giải

Chọn A

Phương pháp giải:

Bước 1: Gọi số cần tìm là $\bar{a b c}$

Tách các bộ số chia hết cho 3, chia 3 dư 1 và chia 3 dư 2.

Bước 2: Xét các trường hợp bộ số chia hết cho 3

+) a, b, c đều chia hết cho 3 $\Rightarrow a, b, c = {3; 6; 9}$

+) $a, b, c \equiv 1 (\mod 3) \Rightarrow a, b, c \in \{1; 4; 7\}$

+) $a, b, c \equiv 2 (\mod 3) \Rightarrow a, b, c \in \{2; 5; 8\}$ .

+) Trong 3 số a, b, c có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2.

Giải chi tiết:

Bước 1:

Gọi số cần tìm là $\bar{a b c}$

Từ các số bài cho ta chia thành 3 bộ số:

+ Bộ số chia hết cho 3 là: 3; 6; 9

+ Bộ số chia cho 3 dư 1 là: 1; 4; 7

+ Bộ số chia cho 3 dư 2 là: 2; 5; 8

Bước 2:

Xét các trường hợp sau:

+) a, b, c đều chia hết cho 3 $\Rightarrow a, b, c = {3; 6; 9}$ Có 3! số.

+) $a, b, c \equiv 1 (\mod 3) \Rightarrow a, b, c \in \{1; 4; 7\}$ => Có 3! số.

+) $a, b, c \equiv 2 (\mod 3) \Rightarrow a, b, c \in \{2; 5; 8\}$ ⇒ Có 3!số.

+) Trong 3 số a, b, c có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2

$3! . C_{3}^{1} . C_{3}^{1} . C_{3}^{1} = 162$

Vậy có 3.3!+162=180 số thỏa mãn đề bài.

Câu 3

Cho một tấm tôn hình vuông có cạnh bằng a. Người ta cắt 4 góc của tấm tôn để được một tấm tôn mới như hình vẽ.

Từ tấm tôn mới, người ta gặp được một hình chóp tứ giác đều. Để khối chóp thu được có thể tích lớn nhất thì diện tích các miếng tốn bỏ đi là

A. $\frac{a^{3}}{3}$

B. $\frac{3 a^{2}}{5}$

C. $\frac{a^{2}}{\sqrt{5}}$

D. $\frac{2 a^{2}}{5}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Một lô hàng có 30 sản phẩm trong đó có 5 phế phẩm. Lấy ngẫu nhiên đồng thời 6 sản phẩm của lô hàng đó. Xác suất để trong 6 sản phẩm lấy ra có không quá 2 phế phẩm là

A. $\frac{2530}{2639}$

B. $\frac{253}{263}$

C. $\frac{253}{280}$

D. $\frac{2535}{2737}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một ô tô đang chạy thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc $v (t) = a - 80 t (m / s)$ trong đó t (giây) là khoảng thời gian tính từ lúc bắt đầu đạp phanh và a là một hằng số dương. Biết rằng từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển được 36m. Khẳng định nào sau đây đúng?

A. aÎ(18,21)

B. aÎ(25,28)

C. aÎ(15,18)

D. aÎ(23,25)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc BAD = 60°. Hình chiếu vuông góc của S lên mặt phẳng đáy là trọng tâm G của tam giác BCD, góc giữa SA và đáy bằng 60°

a) Tính thể tích khối chóp S.ABCD.

b) Tính khoảng cách giữa hai đường thẳng AC và SB.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Hình sau là đồ thị của hàm số $y = \frac{ax+b}{x + c}$ (với $a, b, c \in ℝ$ ).

Khi đó ab - c bằng

A. 0

B. 2

C. -2

D. -1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Hình sau là đồ thị của hàm số $y = \frac{ax+b}{x + c}$ (với $a, b, c \in ℝ$ ).

Khi đó ab - c bằng