Người xưa đã tính đường kính thân cây theo quy tắc “quân bát, phát tam, tồn ngũ, quân nhị”, tức là chu vi thân cây chia làm 8 phần bằng nhau (quân bát); bớt đi 3 phần (phát tam) còn lại 5 phần (tồn ngũ) rồi chia đôi kết quả (quân nhị). Hãy cho biết người xưa đã ước lượng số bằng bao nhiêu?
Người xưa đã tính đường kính thân cây theo quy tắc “quân bát, phát tam, tồn ngũ, quân nhị”, tức là chu vi thân cây chia làm 8 phần bằng nhau (quân bát); bớt đi 3 phần (phát tam) còn lại 5 phần (tồn ngũ) rồi chia đôi kết quả (quân nhị). Hãy cho biết người xưa đã ước lượng số bằng bao nhiêu?
Câu hỏi trong đề: Bài tập Số vô tỉ. Căn bậc hai số học có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi chu vi thân cây và đường kính thân cây là C và d.
Chu vi thân cây chia làm 8 phần, bớt đi 3 phần còn lại là 5 phần, khi đó phần còn lại chiếm chu vi thân cây bằng
Kết quả chia đôi thu được đường kính thân cây nên đường kính thân cây là
Khi đó người xưa đã ước lượng số bằng:
Vậy người xưa đã ước lượng số bằng
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
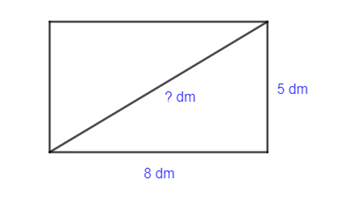
Bình phương độ dài đường chéo của hình chữ nhật là:
82 + 52 = 89.
Độ dài đường chéo của hình chữ nhật là dm.
Có
Làm tròn kết quả đến hàng phần mười được
Vậy độ dài đường chéo của hình chữ nhật đó xấp xỉ 9,4 dm.
Lời giải
a) 81 = 92 và 9 > 0 nên độ dài cạnh của hình vuông là dm.
b) 3600 = 602 và 60 > 0 nên độ dài cạnh của hình vuông là m.
c) Đổi 1 ha = 0,01 km2 = km2 = km2.
Do và nên độ dài cạnh của hình vuông là km = 0,1 km.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập