Trong Bài 10, ta đã dùng cách đo đạc để kiểm nghiệm tính chất sau là đúng:
“Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau” (H.3.45).
Tuy nhiên, đo đạc chỉ cho ta kết quả gần đúng và chỉ trong một trường hợp cụ thể.
Vậy có cách nào để chắc chắn rằng tính chất đó đúng cho mọi trường hợp không?
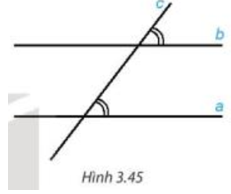
Trong Bài 10, ta đã dùng cách đo đạc để kiểm nghiệm tính chất sau là đúng:
“Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau” (H.3.45).
Tuy nhiên, đo đạc chỉ cho ta kết quả gần đúng và chỉ trong một trường hợp cụ thể.
Vậy có cách nào để chắc chắn rằng tính chất đó đúng cho mọi trường hợp không?
Câu hỏi trong đề: Bài tập Định lí và chứng minh định lí có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
GT |
a // b, c cắt a tại A, c cắt b tại B; là hai góc đồng vị. |
|
KL |
|
Chứng minh:
Qua điểm B kẻ đường thẳng sao cho
Khi đó đường thẳng c tạo với hai đường thẳng a và hai góc đồng vị bằng nhau
Theo dấu hiệu nhận biết hai đường thẳng song song ta có a và song song với nhau. Suy ra qua B có hai đường thẳng b, cùng song song với a. Theo tiên đề Euclid, trùng b. Từ đó suy ra (vì cùng bằng ).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Trong hình vẽ trên, ta có hai đường thẳng a và b song song với nhau.
Đường thẳng c vuông góc với đường thẳng a.
Giao điểm của hai đường thẳng a và b với đường thẳng c lần lượt là A và B.
Do đường thẳng a vuông góc với đường thẳng c nên
Do đường thẳng a song song với đường thẳng b nên (hai góc đồng vị)
Do đó
Vậy đường thẳng b vuông góc với đường thẳng c.
Trong chứng minh này, chúng ta sử dụng các kiến thức về số đo của góc vuông, các góc tạo bởi hai đường thẳng cắt nhau, tính chất hai đường thẳng song song.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
GT |
cắt tại O. và đối đỉnh. |
|
KL |
|
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập