Câu hỏi:

20/05/2022 515

Cho hình chóp S.ABC có mỗi mặt bên là một tam giác vuông và $S A = S B = S C = a$ . Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC; D là điểm đối xứng của S qua P. I là giao điểm của đường thẳng AD với mặt phẳng (SMN). Tính theo a thể tích của khối tứ diện MBSI.

\frac{a^{3}}{12}

\frac{a^{3}}{36}

\frac{a^{3}}{6}

\frac{\sqrt{2} a^{3}}{12}

Xem lời giải

Câu hỏi trong đề: Bộ 15 đề thi Đánh giá năng lực trường ĐHQG HCM năm 2023 - 2024 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn C

Phương pháp giải:

Sử dụng tỉ số diện tích, tỉ số thể tích để tính thể tích khối tứ diện MBSI thông qua thể tích khối tứ diện vuông SABC.

Giải chi tiết:

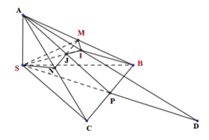
Cho hình chóp S.ABC có mỗi mặt bên là một tam giác vuông và SA=SB=SC=a (ảnh 1)

Do $S A = S B = S C = a$ nên các tam giác $S A B, S B C, S C A \Rightarrow S A, S B, S C$ vuông tại S.

đôi một vuông góc.

Thể tích khối tứ diện vuông S.ABC là: $V = \frac{1}{6} . S A . S B . S C = \frac{a^{3}}{6}$

Gọi J là giao điểm của MN và AP, I là giao điểm của SJ và AD. Khi đó, $I = A D \cap (S M N)$ (do $S I \subset (S M N)$ )

$Δ A S D$ có: P là trung điểm của SD, J là trung điểm của AP.

Xét tam giác vuông SBC có $S P = \frac{1}{2} B C = \frac{a \sqrt{2}}{2} \Rightarrow A P = \sqrt{S A^{2} + S P^{2}} = \frac{a \sqrt{6}}{2}$
$\Rightarrow S J = \frac{1}{2} A P = \frac{a \sqrt{6}}{4}$ .

Ta có: $S D = 2 S P = a \sqrt{2} \Rightarrow A D = a \sqrt{3} \Rightarrow \cos ∠ S D A = \frac{S D}{A D} = \frac{\sqrt{6}}{3}$ .

Áp dụng định lí Menelaus trong tam giác APD ta có:

$\frac{J A}{J P} . \frac{S P}{S D} . \frac{I D}{I A} = 1 \Leftrightarrow 1. \frac{1}{2} . \frac{I D}{I A} = 1 \Leftrightarrow \frac{I D}{I A} = 2 \Leftrightarrow I D = \frac{2}{3} A D = \frac{2 a \sqrt{3}}{3}$

Áp dụng định lí Cosin trong tam giác ta có:

$S I^{2} = S D^{2} + D I^{2} - 2 S D . D I . \cos ∠ S D A = 2 a^{2} + \frac{4}{3} a^{2} - 2. a \sqrt{2} . \frac{2 a \sqrt{3}}{3} . \frac{\sqrt{6}}{3} = \frac{2 a^{2}}{3}$

Dễ dàng chứng minh được:

$S J = \frac{3}{4} S I \Rightarrow S_{Δ S J B} = \frac{3}{4} S_{Δ S I B} \Rightarrow V_{M . S J B} = \frac{3}{4} V_{M . S I B}$ hay $\Rightarrow V_{M . S I B} = \frac{4}{3} V_{M . S J B}$

Lại có: $S_{Δ M J B} = \frac{1}{2} S_{Δ A J B} = \frac{1}{2} . \frac{1}{2} S_{Δ A P B} = \frac{1}{8} S_{Δ A B C}$

$\Rightarrow V_{M . S J B} = \frac{1}{8} V_{S . A B C} \Rightarrow V_{M . S I B} = \frac{4}{3} . \frac{1}{8} V_{S . A B C} = \frac{1}{6} V_{S . A B C} = \frac{1}{6} . \frac{1}{6} a^{3} = \frac{1}{36} a^{3}$

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Phương trình mặt cầu có tâm $I (1; - 2; 3)$ và tiếp xúc với trục Oy là:

A. $x^{2} + y^{2} + z^{2} - 2 x + 4 y - 6 z + 9 = 0.$

B. $x^{2} + y^{2} + z^{2} + 2 x - 4 y + 6 z + 9 = 0.$

x^{2} + y^{2} + z^{2} - 2 x + 4 y - 6 z + 4 = 0.

x^{2} + y^{2} + z^{2} + 2 x - 4 y + 6 z + 4 = 0.

Lời giải

Chọn C

Phương pháp giải:

Mặt cầu tâm $I (x_{0}; y_{0}; z_{0})$ có bán kính R thì có phương trình là ${(x - x_{0})}^{2} + {(y - y_{0})}^{2} + {(z - z_{0})}^{2} = R^{2}$

Giải chi tiết:

Vì mặt cầu tiếp xúc với trục $O y : \{\begin{cases} x = 0 \\ y = t \\ z = 0 \end{cases}$ nên mặt cầu có bán kính $R = d (I; O y)$

Ta có: $\vec{O I} = (1; - 2; 3), \vec{j} = (0; 1; 0) \Rightarrow [\vec{O I}, \vec{j}] = (- 3; 0; 1)$

nên $R = d (I; O y) = \frac{|[\vec{O I}; \vec{j}]|}{|\vec{j}|} = \sqrt{10}$

Phương trình mặt cầu là: ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 10$

$\Leftrightarrow x^{2} + y^{2} + z^{2} - 2 x + 4 y - 6 z + 4 = 0$

Câu 2

Nhân ngày sách Việt Nam, 120 học sinh khối 8 và 100 học sinh khối 9 cùng tham gia phong trào xây dựng “Tủ sách nhân ái”. Sau một thời gian phát động, tổng số sách cả hai khối đã quyên góp được là 540 quyển. Biết rằng mỗi học sinh khối 9 quyên góp nhiều hơn nhiều hơn mỗi học sinh khối 8 một quyển. Hỏi mỗi khối đã quyên góp được bao nhiêu quyển sách? (Mỗi học sinh trong cùng một khối quyên góp số lượng sách như nhau).

A. khối 9 là 240 quyển, khối 8 là 300 quyển.

B. khối 9 là 280 quyển, khối 8 là 260 quyển.

C. khối 9 là 260 quyển, khối 8 là 280 quyển.

D. khối 9 là 300 quyển, khối 8 là 240 quyển.

Lời giải

Phương pháp giải:

Gọi số sách khối 8 và khối 9 quyên góp được lần lượt là x; y (quyển sách), $(0 < x, y < 540, x, y \in ℕ) .$ .

Dựa vào giả thiết của bài toán để lập hệ phương trình và giải hệ phương trình.

+) Phương trình thứ nhất: Số sách lớp 8 + số sách lớp 9 quyên góp được = 540.

+) Phương trình thứ hai: Số sách mỗi học sinh khối 9 – số sách mỗi học sinh khối 8 = 1.

Giải hệ phương trình vừa lập để tìm x; y và kết luận.

Giải chi tiết:

Gọi số sách khối 8 và khối 9 quyên góp được lần lượt là x; y (quyển sách), $(0 < x, y < 540, x, y \in ℕ) .$

Số sách cả hai khối quyên góp được là: $x + y = 540 (1) .$

Số sách một bạn học sinh khối 8 quyên góp là: $\frac{x}{120}$ (quyển)

Số sách một bạn học sinh khối 9 quyên góp là: $\frac{y}{100}$ (quyển)

Mỗi học sinh khối 9 quyên góp nhiều hơn nhiều hơn mỗi học sinh khối 8 một quyển nên ta có phương trình: $\frac{y}{100} - \frac{x}{120} = 1 \Leftrightarrow - 5 x + 6 y = 600 (2) .$

Từ (1) và (2) ta có hệ phương trình:

$\{\begin{cases} x + y = 540 \\ - 5 x + 6 y = 600 \end{cases} \Leftrightarrow \{\begin{cases} 5 x + 5 y = 2700 \\ - 5 x + 6 y = 600 \end{cases} \Leftrightarrow \{\begin{cases} 11 y = 3300 \\ x = 540 - y \end{cases} \Leftrightarrow \{\begin{cases} y = 300 (t m) \\ x = 240 (t m) \end{cases} .$

Vậy khối 9 đã quyên góp được 300 quyển sách, khối 8 đã quyên góp được 240 quyển sách.

Câu 3

What is the main idea of the passage?

A. Advantages of mandatory volunteering programs for students

B. An obligatory volunteer program at high school in Maryland

C. Students of 1997’s attitudes towards obligatory volunteering

D. Volunteering at a variety of organizations in Maryland in USA

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

“Cũng nhà hành viện xưa nay,/ Cũng phường bán thịt cũng tay buôn người” (Truyện Kiều – Nguyễn Du)

Từ nào trong câu thơ trên được dùng với nghĩa chuyển và được chuyển nghĩa theo phương thức nào?

A. “nhà”, chuyển nghĩa theo phương thức hoán dụ

B. “nhà”, chuyển nghĩa theo phương thức ẩn dụ

C. “tay”, chuyển nghĩa theo phương thức hoán dụ

D. “tay” chuyển nghĩa theo phương thức ẩn dụ

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Linda would not win a high price in swimming if she did not maintain her training.

A. Linda is not maintaining her training to score well in swimming.

B. Linda does not want to win a high prize in swimming at all.

C. Linda will win a very high prize in swimming if she maintains her training.

D. Linda joined a swimming contest and tried to win a high prize.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

When I was sick, my best friend took care of me.

A. I had to look after my best friend, who was sick.

B. I was sick when I cared for my best friend.

C. I was cared for by my best friend when I was sick.

D. My best friend was taken care of by me when getting sick.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Phản ứng este hóa giữa axit hữu cơ đơn chức (C_nH_mO₂) và rượu n-propylic thu được hỗn hợp X gồm este, nước, rượu propylic và axit hữu cơ dư. Để có thể loại nước ra khỏi hỗn hợp X, quy trình nào trong các quy trình sau đây là phù hợp?

(I) Cho hỗn hợp trên vào nước, lắc mạnh. Este, axit hữu cơ và rượu propylic không tan trong nước sẽ tách ra khỏi nước.

(II) Cho hỗn hợp trên vào chất làm khan để hút nước.

(III) Đun nóng hỗn hợp đến 100^oC, nước sẽ bay hơi đến khi khối lượng hỗn hợp không đổi thì dừng

(IV) Cho hỗn hợp trên qua dung dịch H₂SO₄ đặc, nước bị giữ lại.

(V) Làm lạnh đến 0^oC, nước sẽ hóa rắn và tách ra khỏi hỗn hợp.

A. (I), (III), (IV), (V).

B. (II).

C. (IV), (V).

D. (I), (II), (III), (IV), (V).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Giáo dục công dân

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học