1) Cho đường thẳng (d): \(y = x - 1\) và parabol (P): \(y = 3{x^2}\).

      a) Tìm tọa độ A thuộc parabol (P) biết điểm A có hoành độ \(x = - 1\).

      b) Tìm b để đường thẳng (d) và đường thẳng (d’): \(y = \frac{1}{2}x + b\) cắt nhau tại một điểm trên trục hoành.

    2) a) Giải hệ phương trình \(\left\{ \begin{array}{l}x + y = 5\\2x - y = 1\end{array} \right.\).

       b) Tìm tham số a để hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x - y = a}\\{7x - 2y = 5a - 1}\end{array}} \right.\). Có nghiệm duy nhất \(\left( {x;y} \right)\) thỏa mãn \(y = 2x\).

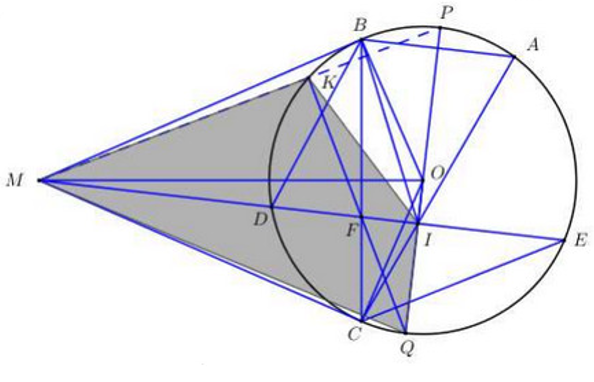
a) Do MB, MC là hai tiếp tuyến của đường tròn (O) nên \(\widehat {OBM} = \widehat {OCM} = {90^0}\)

Xét tứ giác MBOC có: \(\widehat {OBM} + \widehat {OCM} = {180^0}\) suy ra tứ giác MBOC là tứ giác nội tiếp.

b) Xét tam giác FBD và tam giác FEC có:

\(\widehat {BFD} = \widehat {EFC}\left( {dd} \right)\)

\(\widehat {FDB} = \widehat {FCE}\) ( hai góc nội tiếp cùng chắn cung BE)

\( \Rightarrow \Delta FBD \sim \Delta FEC\left( {g - g} \right) \Rightarrow \frac{{FB}}{{FE}} = \frac{{FD}}{{FC}} \Rightarrow FD.FE = FB.FC\left( 1 \right)\)

Ta có AB// ME suy ra \(\widehat {BAC} = \widehat {DIC}\)

Mà \(\widehat {BAC} = \widehat {MBC}\)(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BC)

\( \Rightarrow \widehat {DIC} = \widehat {MBC} \Rightarrow \widehat {MBF} = \widehat {CIF}\)

Xét tam giác FBM và tam giác FIC có:

\(\widehat {BFM} = \widehat {IFC}\) (đđ)

\(\widehat {MBF} = \widehat {CIF}\left( {cmt} \right)\)

\( \Rightarrow \Delta FBM \sim \Delta FIC\left( {g - g} \right) \Rightarrow \frac{{FB}}{{FI}} = \frac{{FM}}{{FC}} \Rightarrow FI.FM = FB.FC\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow FI.FM = FD.FE\left( 3 \right)\)

c) Xét tam giác FDK và tam giác FQE có:

\(\widehat {KFD} = \widehat {EFQ}\) (đđ)

\(\widehat {FKD} = \widehat {FEQ}\)( hai góc nội tiếp cùng chắn cung DQ)

\( \Rightarrow \Delta FKD \sim \Delta FEQ\left( {g - g} \right)\)

\( \Rightarrow \frac{{FK}}{{FE}} = \frac{{FD}}{{FQ}} \Rightarrow FD.FE = FK.FQ\left( 4 \right)\)

Từ (3) và (4) \( \Rightarrow FI.FM = FK.FQ \Leftrightarrow \frac{{FM}}{{FQ}} = \frac{{FK}}{{FI}}\)

Xét tam giác FMQ và tam giác FKI có:

\(\frac{{FM}}{{FQ}} = \frac{{FK}}{{FI}}\left( {cmt} \right)\)

\(\widehat {MFQ} = \widehat {KFI}\)

\( \Rightarrow \Delta FMQ \sim \Delta FKI\left( {c - g - c} \right) \Rightarrow \widehat {FMQ} = \widehat {FKI}\)

Suy ra tứ giác KIQM là tứ giác nội tiếp

\( \Rightarrow \widehat {MQK} = \widehat {MIQ}\)(hai góc nội tiếp cùng chắn cung MQ)

Ta có \(\widehat {MBF} = \widehat {CIF} \Rightarrow \widehat {MBC} = \widehat {MIF}\) suy ra tứ giác MBIC là tứ giác nội tiếp

Mà MOBC là tứ giác nội tiếp nên M, B, O, I, C cùng thuộc 1 đường tròn.

Ta có \(\widehat {OBM} = {90^0}\) suy ra OM là đường kính của đường tròn đi qua 5 điểm M, B, O, I, C.

Suy ra \(\widehat {OIM} = {90^0}\)(góc nội tiếp chắn nửa đường tròn)

\( \Rightarrow IM \bot OI \Rightarrow \widehat {MIQ} = {90^0}\)

\( \Rightarrow \widehat {MKQ} = \widehat {MIQ} = {90^0}\)

Lại có \(\widehat {QKP} = {90^0}\)(góc nội tiếp chắn nửa đường tròn)

Từ đó ta có: \(\widehat {MKP} = \widehat {MKQ} + \widehat {QKP} = {180^0}\)

Vậy 3 điểm P, K, M thẳng hàng.

a)    \(H = \frac{{2{x^2} + 2x}}{{{x^2} - 1}} + \frac{1}{{\sqrt x  + 1}} - \frac{1}{{\sqrt x  - 1}} = \frac{{2x\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} + \frac{1}{{\sqrt x  + 1}} - \frac{1}{{\sqrt x  - 1}}\)

        \( = \frac{{2x}}{{x - 1}} + \frac{1}{{\sqrt x  + 1}} - \frac{1}{{\sqrt x  - 1}} = \frac{{2x}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}} + \frac{1}{{\sqrt x  + 1}} - \frac{1}{{\sqrt x  - 1}}\)

 b)   Theo đề bài ta có \(\sqrt x  - H < 0 \Leftrightarrow \sqrt x  - 2 <  \Leftrightarrow \sqrt x  < 2 \Leftrightarrow x < 4\)

Kết hợp điều kiện \(x \ge 0;x \ne 1\) ta có \(0 \le x < 4;x \ne 1\)

Vậy với \(0 \le x < 4;x \ne 1\) thì \(\sqrt x  - H < 0\)