1. Cho Parabol \(\left( P \right):\,\,y = - {x^2}\) và đường thẳng \(\left( d \right):\,\,y = x - 2\)
a) Vẽ \(\left( P \right)\,\,v{\rm{\`a }}\,\,\left( d \right)\) trên cùng một mặt phẳng tọa độ \[{\rm{Ox}}y\].
b) Viết phương trình đường thẳng \(\left( {d'} \right)\)song song với \(\left( d \right)\) và tiếp xúc với \(\left( P \right)\).
2. Cho phương trình \({x^2} - 4x + m = 0\) (m là tham số)
a) Biết phương trình có một nghiệm bằng \( - 1\). Tính nghiệm còn lại.
b) Xác định m để phương trình có hai nghiệm \({x_1},\,{x_2}\) thỏa mãn \(\left( {3{x_1} + 1} \right)\left( {3{x_2} + 1} \right) = 4\)
1. Cho Parabol \(\left( P \right):\,\,y = - {x^2}\) và đường thẳng \(\left( d \right):\,\,y = x - 2\)
a) Vẽ \(\left( P \right)\,\,v{\rm{\`a }}\,\,\left( d \right)\) trên cùng một mặt phẳng tọa độ \[{\rm{Ox}}y\].
b) Viết phương trình đường thẳng \(\left( {d'} \right)\)song song với \(\left( d \right)\) và tiếp xúc với \(\left( P \right)\).
2. Cho phương trình \({x^2} - 4x + m = 0\) (m là tham số)
a) Biết phương trình có một nghiệm bằng \( - 1\). Tính nghiệm còn lại.
b) Xác định m để phương trình có hai nghiệm \({x_1},\,{x_2}\) thỏa mãn \(\left( {3{x_1} + 1} \right)\left( {3{x_2} + 1} \right) = 4\)
Câu hỏi trong đề: Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất) !!
Quảng cáo
Trả lời:
1.
a) \(\left( P \right):\,\,y = - {x^2}\)
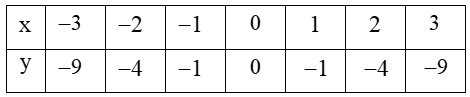
\(\left( d \right):\,\,y = x - 2\)
\(x = 0 \Rightarrow y = - 2:\,\,\,\,\,\,\left( {0; - 2} \right)\)
\(y = 0 \Rightarrow x = 2:\,\,\,\,\,\,\left( {2;0} \right)\)
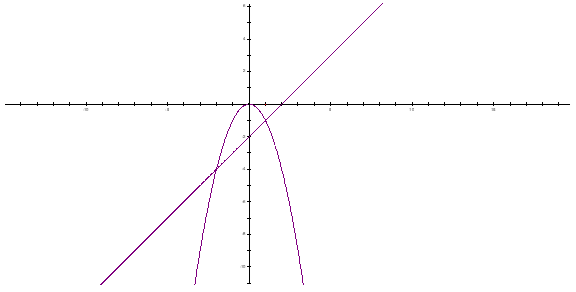
b) Phương trình đường thẳng \(\left( {d'} \right)\) có dạng \(y = {\rm{ax}} + b\)
\(\left( {d'} \right)\)//\(\left( d \right):y = x - 2 \Rightarrow a = 1;\,\,b \ne - 2\)
Phương trình hoành độ giao điểm của \(\left( P \right)\,v{\rm{\`a }}\,\left( {d'} \right)\)là \( - {x^2} = x + b \Leftrightarrow {x^2} + x + b = 0\,\,\left( * \right)\)
PT \(\left( * \right)\) có \(\Delta = 1 - 4b\).
\(\left( P \right)\,v{\rm{\`a }}\,\left( {d'} \right)\)tiếp xúc nhau khi PT \(\left( * \right)\) có nghiệm kép \( \Leftrightarrow \Delta = 0 \Leftrightarrow 1 - 4b = 0 \Leftrightarrow b = \frac{1}{4}\) (nhận).
Vậy PT đường thẳng \(\left( {d'} \right)\,\,l{\rm{\`a }}:\,y = x + \frac{1}{4}\)
2.
a) PT \({x^2} - 4x + m = 0\)có một nghiệm bằng \( - 1\)\( \Rightarrow a - b + c = 0 \Rightarrow 1 + 4 + m = 0 \Rightarrow m = - 5\).
Nghiệm còn lại của PT là \( - \frac{c}{a} = - \frac{m}{1} = - \frac{{ - 5}}{1} = 5\)
b) ĐK \(\Delta ' = {\left( { - 2} \right)^2} - m \ge 0 \Leftrightarrow m \le 4\)
Áp dụng định lí Vi et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 4\\{x_1}{x_2} = m\end{array} \right.\)
\(\begin{array}{l}\left( {3{x_1} + 1} \right)\left( {3{x_2} + 1} \right) = 4 \Rightarrow 9{x_1}{x_2} + 3\left( {{x_1} + {x_2}} \right) + 1 = 4\\ \Rightarrow 9m + 3.4 + 1 = 4 \Rightarrow m = - 1\,\left( {tm} \right)\end{array}\)
Vậy \(m = - 1\) là giá trị cần tìm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
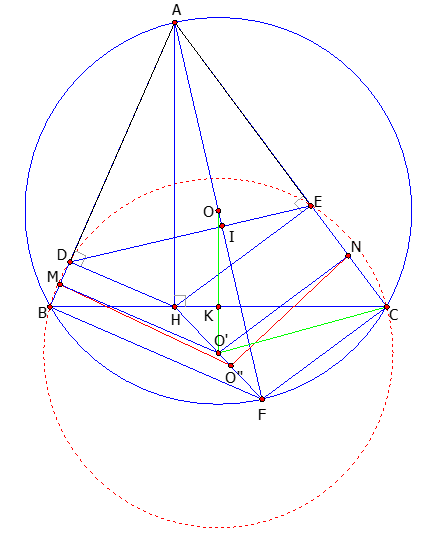
a) Tứ giác AEHD có \(\widehat {ADH} + \widehat {AEH} = {90^0} + {90^0} = {180^0} \Rightarrow \)Tứ giác AEHD nội tiếp được đường tròn đường kính AH.
Tứ giác AEHD (cmt) \(\widehat {ADE} = \widehat {AHE\,}\left( 1 \right)\)(cùng chắn ). Dễ thấy \(\widehat {ACH} = \widehat {AHE\,}\left( 2 \right)\) (cùng phụ \(\widehat {HAE}\)).
Từ (1) và (2) suy ra \(\widehat {ADE} = \widehat {ACH\,}\)nên tứ giác BDEC nội tiếp được đường tròn.
b) Áp dụng hệ thức lượng trong hai tam giác vuông AHB và AHC ta có:
\(\begin{array}{l}B{H^2} = AB.BD \Rightarrow BH = \sqrt {AB.BD} \\H{B^2} = AC.CE \Rightarrow HB = \sqrt {AC.CE} \end{array}\)
Do đó \(BC = BH + HC = \sqrt {AB.BD} + \sqrt {AC.CE} \)
Nối FB, FC. Gọi I là giao điểm của AF và DE.
Ta có \(\widehat {ADE} = \widehat {ACH\,}\) (cmt) và \(\widehat {AFB} = \widehat {ACH\,}\)(cùng chắn ) suy ra \(\widehat {ADE} = \widehat {AFB\,}\)nên tứ giác BDIF nội tiếp được đường tròn\( \Rightarrow \widehat {D{\rm{I}}F} + \widehat {DBF} = {180^0} \Rightarrow \widehat {D{\rm{I}}F} = {180^0} - \widehat {DBF} = {180^0} - {90^0} = {90^0}\). Vậy \[{\rm{A}}F \bot DE\]
c) Gọi M,N,O’’ lần lượt là trung điểm của BD,EC,HF.
– Ta chứng minh được MO’’ và NO’’ lần lượt là đường trung bình của các hình thang BDHF và CEHF\( \Rightarrow MO''//DH\left( 3 \right)\)và \( \Rightarrow NO''//EH\left( 4 \right)\)
– Vì tứ giác BDEC nội tiếp mà\(O'\)là tâm đường tròn ngoại tiếp tam giác BDE suy ra \(O'\)cũng là tâm đường tròn ngoại tiếp tứ giác BDEC\( \Rightarrow O'\) thuộc đường trung trực của BD . Suy ra MO’ là trung trực của BD do đó
\(MO' \bot BD\) lại có \(DH \bot BD\) \( \Rightarrow MO'//DH\left( 5 \right)\).
Tương tự ta có \(NO'//EH\left( 6 \right)\)
Từ (3) và (5) suy ra MO’’ và MO’ là hai tia trùng nhau
Từ (4) và (6) suy ra NO’’ và NO’ là hai tia trùng nhau
Do đó O’ trùng O”. Mà O’’ là trung điểm của HF nên O’ cũng là trung điểm của HF.
d) Trong \(\Delta ABC\) ta có \(\frac{{BC}}{{SinA}} = {\rm{A}}F \Rightarrow SinA = \frac{{BC}}{{{\rm{A}}F}} = \frac{8}{{10}} = \frac{4}{5}\)
Trong \(\Delta ADE\) ta có \(\frac{{DE}}{{SinA}} = {\rm{AH}} \Rightarrow AH = \frac{6}{{\frac{4}{5}}} = 7,5\left( {cm} \right)\)
Vì O’ và O lần lượt là trung điểm của HF và AF nên OO’ là đường trung bình của tam giác AHF\( \Rightarrow {\rm{OO' = }}\frac{{AH}}{2} = \frac{{7,5}}{2} = 3,75\left( {cm} \right)\)
Gọi K là giao điểm của OO’ và BC dễ thấy \[{\rm{OO}}' \bot BC\] tại trung điểm K của BC. Áp dụng định lí Pytago vào tam giác vuông OKC ta tính được \(OK = \sqrt {O{C^2} - K{C^2}} = \sqrt {{5^2} - {4^2}} = 3\left( {cm} \right)\)
Ta có \(KO' = {\rm{OO}}' - OK = 3,75 - 3 = 0,75\left( {cm} \right)\)
Áp dụng định lí Pytago vào tam giác vuông O’KC ta tính được \(O'C = \sqrt {O'{K^2} + K{C^2}} = \sqrt {{{0,75}^2} + {4^2}} = \frac{{\sqrt {265} }}{4}\left( {cm} \right)\)
Vậy bán kính đường trò (O’) là \(\frac{{\sqrt {265} }}{4}\left( {cm} \right)\).
Lời giải
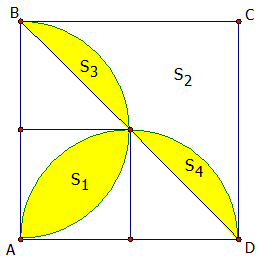
Gọi a là cạnh hình vuông ABCD. Ta cm được:
\({S_3} = {S_4} = \frac{{{{\left( {\frac{a}{2}} \right)}^2}.\pi .90}}{{360}} - \frac{1}{2} \cdot {\left( {\frac{a}{2}} \right)^2} = \frac{{{a^2}}}{4}\left( {\frac{\pi }{4} - \frac{1}{2}} \right)\)
\({S_1} = {S_3} + {S_4} = \frac{{{a^2}}}{4}\left( {\frac{\pi }{4} - \frac{1}{2}} \right) + \frac{{{a^2}}}{4}\left( {\frac{\pi }{4} - \frac{1}{2}} \right) = \frac{{{a^2}}}{2}\left( {\frac{\pi }{4} - \frac{1}{2}} \right)\)
\({S_2} = \frac{1}{2}{a^2} - \frac{{{a^2}}}{2}\left( {\frac{\pi }{4} - \frac{1}{2}} \right) = \frac{{{a^2}}}{2}\left( {\frac{3}{2} - \frac{\pi }{4}} \right)\)
Do đó \(\frac{{{S_1}}}{{{S_2}}} = \frac{{\frac{{{a^2}}}{2}\left( {\frac{\pi }{4} - \frac{1}{2}} \right)}}{{\frac{{{a^2}}}{2}\left( {\frac{3}{2} - \frac{\pi }{4}} \right)}} = \frac{{\pi - 2}}{{6 - \pi }}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.