Câu hỏi:
12/07/2024 4,448
1) Cho biểu thức: A = (2x - 3)2 - (x + 1)(x + 5) + 2
Rút gọn và tìm giá trị nhỏ nhất của A.
2) Cho B = n2 - 27n2 + 121. Tìm số tự nhiên n để B là số nguyên.
1) Cho biểu thức: A = (2x - 3)2 - (x + 1)(x + 5) + 2
Rút gọn và tìm giá trị nhỏ nhất của A.
2) Cho B = n2 - 27n2 + 121. Tìm số tự nhiên n để B là số nguyên.
Câu hỏi trong đề: Đề kiểm tra Giữa kì 1 Toán 8 có đáp án (Mới nhất) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
1) A = (2x - 3)2 - (x + 1)(x + 5) + 2
= 4x2 - 12x + 9 - x2 - 6x - 5 + 2 = 3x2 - 18x + 6 = 3(x2 - 6x + 2)
= 3[(x - 3)2 - 7] ≥ 3.(-7) = -21
Dấu "=" xảy ra khi x - 3 = 0 ⇔ x = 3. Vậy MinA = -21 ⇔ x = 3
2) B = n4 - 27n2 + 121 = n4 + 22n2 + 121 - 49n2
= (n2 + 11)2 - (7n)2 = (n2 + 7n + 11)(n2 - 7n + 11)
Vì n ∈ N nên n2 -7n + 11 là số tự nhiên lớn hơn 1
Điều kiện cần để B là số nguyên tố là:
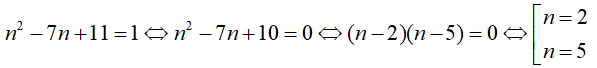
- Với n = 2 thì B = 29 (là số nguyên tố)
- Với n = 5 thì B = 71 (là số nguyên tố)
Vậy n ∈ {2, 5} là các giá trị cần tìm.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a. Vì ABCD là hình thang vuông nên ∠A = ∠D = 90o
⇒ AD ⊥ DC tại D (1)
Xét tam giác HDC ta có:
NH = ND (giả thiết)
MH = Mc (giả thiết)
⇒ NM là đường trung bình của tam giác HDC
⇒ NM // DC (2)
Từ (1) và (2) suy ra MN ⊥ AD tại G (từ vuông góc đến song song)
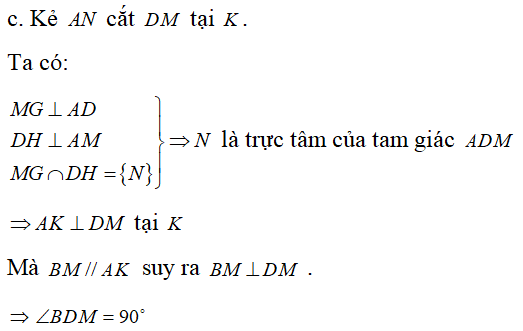
Lời giải
a. 2x2 - 3x - 2 = 2x2 - 4x + x - 2 = (2x2 - 4x) + (x - 2)
= 2x(x - 2) + (x - 2) = (x - 2)(2x + 1)
b. 4x(x - 2) + 3(2 - x) = 4x(x - 2) - (x - 2) = (x - 2)(4x - 1)
c. 27x3 + 8 = (3x)3 + 23 = (3x + 2)[(3x)2 - 2.3x + 22] = (3x + 2)(9x2 - 6x + 2)
d. x2 + 2x - y2 + 1 = (x2 + 2x + 1) - y2 = (x + 1)2 - y2
= (x + 1 - y)(x + 1 + y)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo