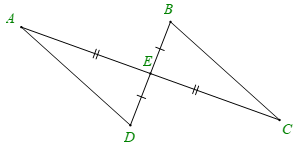
Cho tam giác ABC có AB = AC . Trên cạnh AB và AC lấy các điểm D, E sao cho AD = AE. Gọi K là giao điểm của BE và CD. Chọn câu sai.

Đáp án đúng là: D

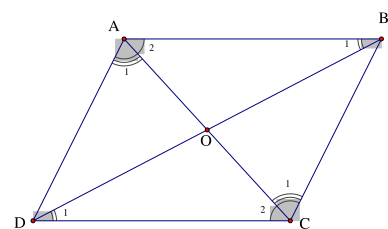
Xét \[\Delta ABC\] và \[\Delta MNP\] có:

AB = PN

\(\widehat A = \widehat P\)

AC = PM

Suy ra \[\Delta ABC = \Delta PNM\] (c.g.c)

(Trong đó:

Đỉnh A tương ứng với đỉnh P.

Đỉnh B tương ứng với đỉnh N.

Đỉnh C tương ứng với đỉnh M)

Đáp án đúng là: C

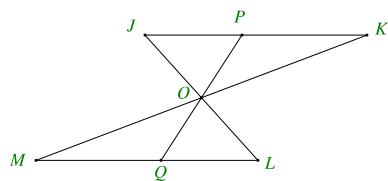
+ Vì

\[AB{\rm{//}}DC\] nên \[\widehat {{A_2}} = \widehat {{C_2}}\]; \[\widehat {{B_1}} = \widehat {{D_1}}\] (2 góc so le trong)

+ Vì \[AD{\rm{//}}BC\] nên \[\widehat {{A_1}} = \widehat {{C_1}}\] (2 góc so le trong)

+ Xét \[\Delta ABC\] và \[\Delta CDA\] có:

\[\widehat {{A_2}} = \widehat {{C_2}}\] (cmt)

AC là cạnh chung

\[\widehat {{C_1}} = \widehat {{A_1}}\] (cmt)

\[ \Rightarrow \Delta ABC = \Delta CDA\] (g.c.g)

Suy ra AB = DC; AD = BC (hai cạnh tương ứng)

(A và B sai)

+ Xét \[\Delta ABO\] và \[\Delta CDO\] có:

\[\widehat {{A_2}} = \widehat {{C_2}}\] (cmt)

AB = DC (cmt)

\[\widehat {{B_1}} = \widehat {{D_1}}\] (cmt)

\[ \Rightarrow \Delta ABO = \Delta CDO\] (g.c.g)

Suy ra OA = OC; OB = OD (2 cạnh tương ứng)

(C đúng, D sai)