Một bạn học sinh đi học từ nhà đến trường với vận tốc trung bình 4 km/h. Sau khi đi được 23quãng đường, bạn ấy đã tăng vận tốc lên 5 km/h. Tính quãng đường từ nhà đến trường của bạn học sinh đó, biết...

Gọi x (km) là quãng đường từ nhà đến trường của bạn học sinh (x > 0). Quãng đường đi với vận tốc 4 km/h là 23x (km). Thời gian đi 23 quãng đường đó là: 23x:4=x6 (giờ). Quãng đường đi với vận tốc 5 km/h là 13x (km). Thời gian đi 13 quãng đường còn lại là: 13x:5=x15 (giờ). Đổi 28 phút = 715 giờ. Thời gian đi hết quãng đường là 28 phút hay 715 giờ nên ta có phương trình: x6+x15=715 ⇔x2+x5=75 ⇔5x10+2x10=1410 Û 5x + 2x = 14 Û 7x = 14 Û x = 2 (TMĐK). Vậy quãng đường từ nhà đến trường của bạn học sinh đó là 2 km.

Câu hỏi:

13/07/2024 501

Một bạn học sinh đi học từ nhà đến trường với vận tốc trung bình 4 km/h. Sau khi đi được $\frac{2}{3}$ quãng đường, bạn ấy đã tăng vận tốc lên 5 km/h. Tính quãng đường từ nhà đến trường của bạn học sinh đó, biết rằng thời gian bạn ấy đi từ nhà đến trường là 28 phút.

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi x (km) là quãng đường từ nhà đến trường của bạn học sinh (x > 0).

Quãng đường đi với vận tốc 4 km/h là $\frac{2}{3} x$ (km).

Thời gian đi $\frac{2}{3}$ quãng đường đó là: $\frac{2}{3} x : 4 = \frac{x}{6}$ (giờ).

Quãng đường đi với vận tốc 5 km/h là $\frac{1}{3} x$ (km).

Thời gian đi $\frac{1}{3}$ quãng đường còn lại là: $\frac{1}{3} x : 5 = \frac{x}{15}$ (giờ).

Đổi 28 phút = $\frac{7}{15}$ giờ.

Thời gian đi hết quãng đường là 28 phút hay $\frac{7}{15}$ giờ nên ta có phương trình:

$\frac{x}{6} + \frac{x}{15} = \frac{7}{15}$

$\Leftrightarrow \frac{x}{2} + \frac{x}{5} = \frac{7}{5}$

$\Leftrightarrow \frac{5 x}{10} + \frac{2 x}{10} = \frac{14}{10}$

Û 5x + 2x = 14

Û 7x = 14

Û x = 2 (TMĐK).

Vậy quãng đường từ nhà đến trường của bạn học sinh đó là 2 km.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm. Kẻ đường cao AH.

a) Chứng minh: DABC đồng dạng với DHBA.

b) Chứng minh: AH² = HB . HC.

c) Tính độ dài các cạnh BC, AH.

d) Phân giác của góc ACB cắt AH tại E, cắt AB tại D. Tính tỉ số diện tích của hai tam giác ACD và HCE.

Xem đáp án

Lời giải

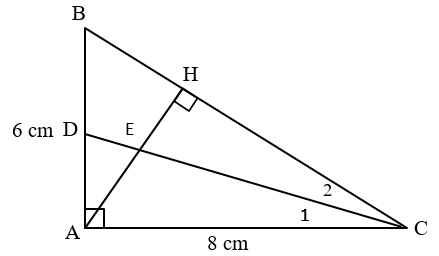
Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm. Kẻ đường cao AH. a) Chứng minh: ABC đồng dạng với HBA. b) Chứng minh: AH2 = HB . HC. c) Tính độ dài các cạnh BC, AH. d) Phân giác của góc ACB cắt AH tại E, cắt AB tại D. Tính tỉ số diện tích của hai tam giác ACD và HCE. (ảnh 1)

a) Xét DABC và DHBA có:

$\hat{B A C} = \hat{A H B} = 90^{o}$

chung

Do đó DABC DHBA (g.g).

b) Chứng minh: AH² = HB . HC.

Xét DABH và DCAH có:

$\hat{A H B} = \hat{A H C} = 90^{o}$ (vì $A H ⊥ B C$ ).

$\hat{B A H} = \hat{A C H}$ (cùng phụ $\hat{C A H}$ ).

Do đó DABH DCAH (g.g).

c) Áp dụng định lý Py-ta-go vào DABC vuông tại A, ta có:

$B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{6^{2} + 8^{2}} = 10$ (cm).

Từ câu a: DABC DHBA nên: $\frac{A C}{H A} = \frac{B C}{B A}$ .

Suy ra: $H B = \frac{A B^{2}}{B C} = \frac{6^{2}}{10} = 3,6$ (cm).

Vậy BC = 10 cm; AH = 4,8 cm.

d) Từ câu a: DABC DHBA nên: $\frac{A B}{H B} = \frac{B C}{B A}$ .

Suy ra: $\hat{C A D} = \hat{A H C} = 90^{o}$ (cm).

Do đó: HC = BC – HB = 10 – 3,6 = 6,4 (cm).

Xét DACD và DHCE có:

$\hat{C A D} = \hat{A H C} = 90^{o}$

${\hat{C}}_{1} = {\hat{C}}_{2}$ (vì CD là tia phân giác của $\hat{A C B}$ )

Do đó DACD

Suy ra $\frac{S_{A C D}}{S_{H C E}} = {(\frac{A C}{H C})}^{2} = {(\frac{8}{6,4})}^{2} = \frac{25}{16}$ .

Câu 2

Cho ba số x, y, z dương và đôi một khác nhau thỏa mãn $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 0.$ Tính giá trị của biểu thức: $A = \frac{y z}{x^{2} + 2 y z} + \frac{x z}{y^{2} + 2 x z} + \frac{x y}{z^{2} + 2 x y}$ .

Xem đáp án

Lời giải

Ta có: $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 0 \Leftrightarrow \frac{x y + y z + x z}{x y z} = 0$ .

Mà ba số x, y, z dương nên: xyz > 0.

Nên: xy + yz + xz = 0

Û yz = – xy – xz.

Ta có: x²+ 2yz = x²+ yz – xy – xz

= x(x – y) – z(x – y) = (x – y)(x – z).

Tương tự: y²+ 2xz = (y – x)(y – z);

z²+ 2xy = (z – x)(z – y).

Do đó: $A = \frac{y z}{x^{2} + 2 y z} + \frac{x z}{y^{2} + 2 x z} + \frac{x y}{z^{2} + 2 x y}$

$= \frac{y z}{(x - y) (x - z)} + \frac{x z}{(y - x) (y - z)} + \frac{x y}{(z - x) (z - y)}$

$= \frac{- y z (y - z)}{(x - y) (y - z) (z - x)} - \frac{x z (z - x)}{(x - y) (y - z) (z - x)} - \frac{x y (x - y)}{(x - y) (y - z) (z - x)}$

$= \frac{- y z (y - z) - x z (z - x) - x y (x - y)}{(x - y) (y - z) (z - x)}$

$= \frac{- y z (y - z) + x z (y - z) + x z (x - y) - x y (x - y)}{(x - y) (y - z) (z - x)}$

$= \frac{(y - z) (x z - y z) + (x - y) (x z - x y)}{(x - y) (y - z) (z - x)}$

$= \frac{z (x - y) (y - z) - x (x - y) (y - z)}{(x - y) (y - z) (z - x)}$

$= \frac{(x - y) (y - z) (z - x)}{(x - y) (y - z) (z - x)} = 1$ .

Vậy $A = \frac{y z}{x^{2} + 2 y z} + \frac{x z}{y^{2} + 2 x z} + \frac{x y}{z^{2} + 2 x y} = 1$ .

Câu 3

Tính diện tích toàn phần và thể tích của hình lăng trụ đứng có đáy là tam giác vuông theo các kích thước ở hình sau:

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Giải các phương trình và bất phương trình sau:

a) |x + 5| = 3x + 1;

b) $\frac{x + 6}{5} - \frac{x - 2}{3} < 2$ ;

c) $\frac{x - 2}{x + 2} - \frac{3}{x - 2} = \frac{2 (x - 11)}{x^{2} - 4}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho ba số x, y, z dương và đôi một khác nhau thỏa mãn 1x+1y+1z=0. Tính giá trị của biểu thức: A=yzx2+2yz+xzy2+2xz+xyz2+2xy.

Tính diện tích toàn phần và thể tích của hình lăng trụ đứng có đáy là tam giác vuông theo các kích thước ở hình sau:

Giải các phương trình và bất phương trình sau: a) |x + 5| = 3x + 1; b) x+65−x−23<2; c) x−2x+2−3x−2=2(x−11)x2−4

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho ba số x, y, z dương và đôi một khác nhau thỏa mãn $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 0.$ Tính giá trị của biểu thức: $A = \frac{y z}{x^{2} + 2 y z} + \frac{x z}{y^{2} + 2 x z} + \frac{x y}{z^{2} + 2 x y}$ .

Giải các phương trình và bất phương trình sau:

a) |x + 5| = 3x + 1;

b) $\frac{x + 6}{5} - \frac{x - 2}{3} < 2$ ;

c) $\frac{x - 2}{x + 2} - \frac{3}{x - 2} = \frac{2 (x - 11)}{x^{2} - 4}$