Câu hỏi trong đề: Đề kiểm tra Giữa kì 2 Toán 7 có đáp án (Mới nhất) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Bậc của đa thức là bậc cao nhất của hạng tử.
Hạng tử 3a5 có bậc cao nhất là 5.
Do đó bậc của đa thức đã cho là 5.
Vậy chọn A.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
GT |
∆ABC vuông tại A, \[\widehat B = {60^o}\], AB = 5cm. BD là tia phân giác \(\widehat {ABC}\) (\(D \in AC\)). \(DE \bot BC\,\,(E \in BC)\). |
|
KL |
a) ∆ADB = ∆BDE. b) ∆AEB là tam giác đều. c) Tính BC. |
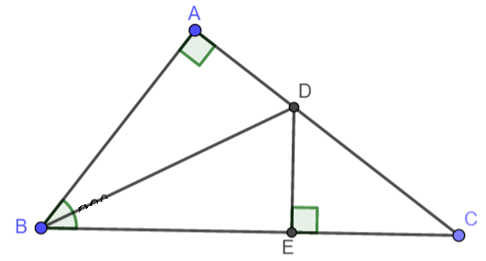
a) Xét ∆ABD vuông tại A và ∆BDE vuông tại E có:
BD cạnh chung.
\[\widehat {ABD} = \widehat {DBE} = {30^o}\](BD là phân giác góc B)
Do đó ∆ADB = ∆BDE (cạnh huyền – góc nhọn).
b) Từ câu a: ∆ADB = ∆BDE suy ra AB = BE.
Xét ∆ABE có AB = BE, \(\widehat B = {60^o}\).
Vậy ∆ABE là tam giác đều.
c) Ta có ∆ABE là tam giác đều (câu b)
Suy ra AB = BE = AE = 5 cm (*)
Do đó \[\widehat {BAE} = \widehat {ABE} = {60^o}\]
Mặt khác \[\widehat {BAC} = {90^o}\]
\[ \Rightarrow \widehat {EAC} = \widehat {BAC} - \widehat {BAE} = {90^o} - {60^o} = {30^o}\] (1)
Áp dụng định lý tổng ba góc của một tam giác vào ∆ABC, ta có:
\[\widehat {ABC} + \widehat {BCA} + \widehat {BAC} = {180^o}\]
\[ \Rightarrow \widehat {BCA} = {180^o} - \widehat {ABC} - \widehat {BAC}\]
\[ \Rightarrow \widehat {BCA} = {180^o} - {60^o} - {90^o} = {30^o}\] (2)
Từ (1) và (2) suy ra \[\widehat {EAC} = \widehat {BCA}\] nên ∆AEC cân tại E.
Suy ra AC = EC = 5 cm (**)
Từ (*) và (**) suy ra BC = BE + EC = 5 + 5 = 10 (cm).
Vậy BC = 10 cm.
Lời giải
a) Ta có: \[A = \left( {\frac{{ - 1}}{2}{x^2}{y^3}z} \right)\,\,.\,\,\left( {\frac{{ - 14}}{3}x{y^2}{z^2}} \right)\]
\[ = \left( {\frac{{ - 1}}{2}\,.\,\,\frac{{ - 14}}{3}} \right).\,\left( {{x^2}.\,x} \right).\,\left( {{y^3}.\,{y^2}} \right)\left( {z\,.\,{z^2}} \right)\]
\[ = \frac{7}{3}\,.\,{x^{2\, + \,1}}.\,\,{y^{3\, + \,2}}.\,{z^{1\, + \,2}}\]
\[ = \frac{7}{3}{x^3}{y^5}{z^3}\].
Vậy \[A = \frac{7}{3}{x^3}{y^5}{z^3}\].
b) Đơn thức A có hệ số là \[\frac{7}{3}\].
Đơn thức \[\frac{7}{3}{x^3}{y^5}{z^3}\], biến x có số mũ là 3; biến y có số mũ là 5; biến z có số mũ là 3.
Tổng số mũ của các biến là 3 + 5 + 3 = 11.
Vậy đơn thức A có hệ số là \[\frac{7}{3}\] và có bậc là 11.
c) Thay x = 1; y = −1; z = 2 vào biểu thức A, ta được:
\[A = \frac{7}{3}{x^3}{y^5}{z^3} = \frac{7}{3}\,.\,{1^3}\,.\,{( - 1)^5}\,.\,{2^3} = - \frac{{56}}{3}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
Đề thi giữa học kì 2 Toán 7 KNTT - Đề 01 có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận