Cho f(x)=ax3+bx2+cx+d trong đó a, b, c, d∈ℤ và thỏa mãn b = 3a + c. Chứng minh rằng f(1).f(-2) là bình phương của một số nguyên.

Ta có f(1)=a+b+c+d. Suy ra f(1)−f(−2)=9a−3b+3c. Mà b=3a+c suy ra f(1)−f(−2)=9a−33a+c+3c=9a−9a−3c+3c=0 ⇒f(1)=f(−2). Suy ra f(1).f(−2)=f(1)2=a+b+c+d2. Mà a, b, c, d∈ℤ nên a+b+c+d∈ℤ hay a+b+c+d2 là bình phương của một số nguyên. Suy ra điều phải chứng minh.

Câu hỏi:

13/07/2024 532

Cho $f (x) = a x^{3} + b x^{2} + c x + d$ trong đó $a, b, c, d \in ℤ$ và thỏa mãn b = 3a + c. Chứng minh rằng f(1).f(-2) là bình phương của một số nguyên.

Xem lời giải

Câu hỏi trong đề: Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có $f (1) = a + b + c + d .$

Suy ra $f (1) - f (- 2) = 9 a - 3 b + 3 c .$

Mà $b = 3 a + c$ suy ra $f (1) - f (- 2) = 9 a - 3 (3 a + c) + 3 c = 9 a - 9 a - 3 c + 3 c = 0$

$\Rightarrow f (1) = f (- 2) .$

Suy ra $f (1) . f (- 2) = {[f (1)]}^{2} = {(a + b + c + d)}^{2} .$

Mà

a, b, c, d \in ℤ

nên

a + b + c + d \in ℤ

hay

{(a + b + c + d)}^{2}

là bình phương của một số nguyên. Suy ra điều phải chứng minh.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC có AB = 6 cm; AC = 8 cm; BC = 10 cm.

a) Chứng minh tam giác ABC vuông tại A.

b) Vẽ tia phân giác BD của góc ABC (D thuộc AC), từ D vẽ DE ^ BC (E Î BC).

Chứng minh DA = DE.

c) Kéo dài ED và BA cắt nhau tại F. Chứng minh DF > DE.

d) Chứng minh đường thẳng BD là đường trung trực của đoạn thẳng FC.

Xem đáp án

Lời giải

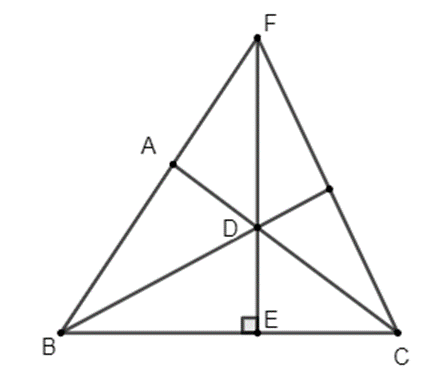
Cho tam giác ABC có AB = 6 cm; AC = 8 cm; BC = 10 cm. a) Chứng minh tam giác ABC vuông tại A. b) Vẽ tia phân giác BD của góc ABC (D thuộc AC), từ D vẽ DE  BC (E  BC). Chứng minh DA = DE. c) Kéo dài ED và BA cắt nhau tại F. Chứng minh DF > DE. d) Chứng minh đường thẳng BD là đường trung trực của đoạn thẳng FC. (ảnh 1)

a) Ta có AB = 6(cm) (gt); AC = 8(cm) (gt) nên

AB² + AC² = 6²+ 8² =100 (cm) (1)

Mà BC = 10(cm) (gt) nên BC² = 10² = 100 (cm) (2)

Từ (1) và (2) suy ra AB² + AC² = BC²

Xét tam giác ABC có AB² + AC² = BC²(chứng minh trên) nên tam giác ABC vuông tại A (Định lí Pytago đảo). (1 điểm)

b) Vì BD là phân giác của góc ABC; DA, DE lần lượt là khoảng cách từ D đến AB, BC

Suy ra DA = DE (tính chất tia phân giác của một góc) (1 điểm)

c) Tam giác ADF vuông tại A nên DF > AD

Lại có AD = DE (chứng minh trên) nên DF > DE (0,5 điểm)

d) Ta có: (tam giác ABD vuông tại A)

(tam giác EBD vuông tại E)

Mà (BD là tia phân giác của góc ABC)

Do đó:

Lại có (hai góc đối đỉnh)

Suy ra

Xét tam giác BDF và tam giác BDC có:

BD cạnh chung

(BD là tia phân giác của góc ABC)

(chứng minh trên)

Do đó: (g.c.g)

BF = BC suy ra B thuộc đường trung trực FC (3)

Và DF = DC suy ra D thuộc đường trung trực FC (4)

Từ (3) và (4) suy ra BD là đường trung trực của FC.

Câu 2

Cho hai đa thức

$f (x) = - {2x}^{2} - {3x}^{3} - 5x + {5x}^{3} - x + x^{2} + 4x + 3 + {4x}^{2}$

$g (x) = {2x}^{2} - x^{3} + 3x + {3x}^{3} + x^{2} - x - 9x + 2.$

a) Tìm $h (x) = f (x) - g (x)$

b) Tìm nghiệm của đa thức h(x).

Xem đáp án

Lời giải

a, $f (x) = - {2x}^{2} - {3x}^{3} - 5x + {5x}^{3} - x + x^{2} + 4x + 3 + {4x}^{2}$

$= (- 3 x^{3} + 5 x^{3}) + (- 2 x^{2} + x^{2} + 4 x^{2}) + (- 5 x - x + 4 x) + 3$

$= 2 x^{3} + 3 x^{2} - 2 x + 3$

$g (x) = {2x}^{2} - x^{3} + 3x + {3x}^{3} + x^{2} - x - 9x + 2.$ $= (- x^{3} + 3 x^{3}) + (2 x^{2} + x^{2}) + (3 x - x - 9 x) + 2$

$= 2 x^{3} + 3 x^{2} - 7 x + 2$

Ta có: $h (x) = f (x) - g (x)$ $= (2 x^{3} + 3 x^{2} - 2 x + 3) - (2 x^{3} + 3 x^{2} - 7 x + 2)$

$= 2 x^{3} + 3 x^{2} - 2 x + 3 - 2 x^{3} - 3 x^{2} + 7 x - 2$

$= (2 x^{3} - 2 x^{3}) + (3 x^{2} - 3 x^{2}) + (- 2 x + 7 x) + (3 - 2)$

$= 5 x + 1$

Ta có h(x) = 0 hay 5x + 1 = 0

$\Rightarrow 5 x = - 1 \Rightarrow x = \frac{- 1}{5}$

Vậy

x = \frac{- 1}{5}

l à n g h i ệ m c ủ a đ a t h ứ c h (x) .

Câu 3

a) Tìm $x \in ℝ$ , biết $|\frac{1}{4} + x| = \frac{5}{6}$

b) Tính giá trị của biểu thức $A = {5x}^{2} - 3x - 16$ khi x = 2

c) Cho đơn thức $A = 4 x^{2} y^{2} {(- 2 x^{3} y^{2})}^{2}$ . Hãy thu gọn và chỉ ra hệ số, phần biến và bậc của đơn thức A.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Thực hiện các phép tính sau:

a) $\frac{- 18}{24} + \frac{15}{- 21}$

b) $9 - 3, 6 - 4, 1 - (- 1, 3)$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho f(x)=ax3+bx2+cx+d trong đó a, b, c, d∈ℤ và thỏa mãn b = 3a + c. Chứng minh rằng f(1).f(-2) là bình phương của một số nguyên.

Cho hai đa thức fx = −2x2− 3x3− 5x + 5x3− x + x2+ 4x + 3 + 4x2 gx = 2x2− x3+ 3x + 3x3+ x2− x − 9x + 2. a) Tìm hx = fx − gx b) Tìm nghiệm của đa thức h(x).

a) Tìm x∈ℝ , biết 14+x=56 b) Tính giá trị của biểu thức A = 5x2– 3x – 16 khi x = 2 c) Cho đơn thức A=4x2y2−2x3y22. Hãy thu gọn và chỉ ra hệ số, phần biến và bậc của đơn thức A.

Thực hiện các phép tính sau: a) −1824+15−21 b) 9−3,6−4,1−−1,3

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho $f (x) = a x^{3} + b x^{2} + c x + d$ trong đó $a, b, c, d \in ℤ$ và thỏa mãn b = 3a + c. Chứng minh rằng f(1).f(-2) là bình phương của một số nguyên.

Cho hai đa thức

$f (x) = - {2x}^{2} - {3x}^{3} - 5x + {5x}^{3} - x + x^{2} + 4x + 3 + {4x}^{2}$

$g (x) = {2x}^{2} - x^{3} + 3x + {3x}^{3} + x^{2} - x - 9x + 2.$

a) Tìm $h (x) = f (x) - g (x)$

b) Tìm nghiệm của đa thức h(x).

a) Tìm $x \in ℝ$ , biết $|\frac{1}{4} + x| = \frac{5}{6}$

b) Tính giá trị của biểu thức $A = {5x}^{2} - 3x - 16$ khi x = 2

c) Cho đơn thức $A = 4 x^{2} y^{2} {(- 2 x^{3} y^{2})}^{2}$ . Hãy thu gọn và chỉ ra hệ số, phần biến và bậc của đơn thức A.

Thực hiện các phép tính sau:

a) $\frac{- 18}{24} + \frac{15}{- 21}$

b) $9 - 3, 6 - 4, 1 - (- 1, 3)$