khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 7
  3. Toán

Câu hỏi:

19/08/2025 756 Lưu

Thời gian làm xong bài tập Toán (tính bằng phút) của 30 học sinh lớp 7B được giáo viên ghi lại trong bảng sau:

Thời gian (x)

5

7

8

9

10

13

 

Tần số (n)

4

3

9

7

5

2

N = 30

          a) Dấu hiệu ở đây là gì? Tìm mốt của dấu hiệu?

          b) Tính số trung bình cộng của dấu hiệu?

Xem lời giải

Câu hỏi trong đề: Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

a) Dấu hiệu ở đây là: "Thời gian làm xong bài tập Toán (tính bằng phút) của học sinh lớp 7B".      (0,5 điểm)

Mốt của dấu hiệu là: M0 = 8      (0,5 điểm)

b) Trung bình cộng của dấu hiệu là:

X = 5.4+7.3+8.9+9.7+10.5+13.230= 8,4

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm số tự nhiên n có hai chữ số biết rằng 2n + 1 và 3n + 1 đồng thời là hai số chính phương.

Lời giải

Vì n có hai chữ số nên 10  n  99  20  2n  198  21  2n + 1  199.

Vì 2n + 1 là số chính phương mà 21  2n + 1  199 nên 2n + 1 {25; 36; 49; 64; 81; 100; 121; 144; 169; 196}.

Vì 2n + 1 lẻ nên 2n + 1 {25; 49; 81; 121; 169}  n {12; 24; 40; 60; 84} (1)

Vì 3n + 1 cũng là một số chính phương nên từ (1)  n = 40.

Câu 2

Cho ΔABC, lấy M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:

          a) AC = EB và AC // BE;

          b) Trên AC lấy điểm I, trên EB lấy điểm K sao cho AI = EK;

          Chứng minh ba điểm: I, M, K thẳng hàng.

c) Từ E kẻ EH ⊥ BC (H ∈ BC). Giả sử K là trung điểm của BE và HK = 5 cm; HE = 6 cm. Tính độ dài đoạn thẳng BH.

Lời giải

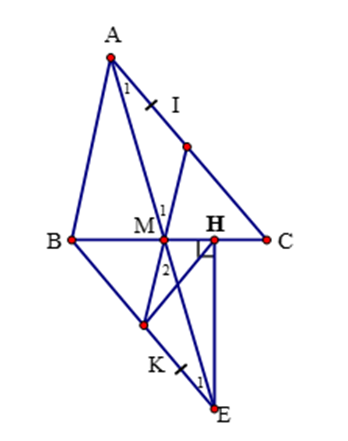
Cho ABC, lấy M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:           a) AC = EB và AC // BE;           b) Trên AC lấy điểm I, trên EB lấy điểm K sao cho AI = EK;           Chứng minh ba điểm: I, M, K thẳng hàng. c) Từ E kẻ EH  BC (H  BC). Giả sử K là trung điểm của BE và HK = 5 cm; HE = 6 cm. Tính độ dài đoạn thẳng BH. (ảnh 1)

a) Xét tam giác AMC và tam giác EMB có:

                    MA = ME (GT)

                 AMC^=EMB^    (Hai góc đối đỉnh)

                    MC = MB (M là trung điểm của BC)

Do đó:  tam giác AMC = tam giác EMB (c – g – c)

 => AC = EB (Hai cạnh tương ứng)     (1 điểm)

và A^1=E^1   (Hai góc tương ứng)

Mà A^1  và  E^1  ở vị trí so le trong nên AC // BE        
b) 

Xét  Δ AMI và  Δ EMK có:

                    AI = EK (GT)

                  A^1=E^1 (CM ở câu a)     

                    MA = ME (GT)

Do đó: AMI = EMK (c – g – c)

=> M^1=M^2 (hai góc tương ứng)

Ta có: M^1+IME^= 1800 (Hai góc kề bù) nên M^2+IME^   = 1800

 Ba điểm I, M, K thẳng hàng.         
c)

Vì Δ BHE vuông tại H có HK là đường trung tuyến (do K là trung điểm của BE)

 Nên HK =  

 BE = 2HK = 2.5 = 10 cm.

Áp dụng định lý Pytago vào tam giác  BHE vuông tại H có:

          BE2 = BH2 + HE2

          102 = BH2 + 62

        =>   BH2 = 100 – 36 = 64

        =>    BH = 8 cm 

Câu 3

P(x) = 2x4 + 9x2 – 3x + 7 – x – 4x2 – 2x4

          Q(x) = – 5x3 – 3x – 3 + 7x – x2 – 2 

a) Thu gọn các đa thức trên và sắp xếp các hạng tử theo lũy thừa giảm dần của biến. Tìm bậc của mỗi đa thức trên;

b, Tính giá trị của các đa thức P(x) tại x = −12  ; Q(x) tại x = 1;

c, Tính Q(x) + P(x) và Q(x) – P(x);

d, Tìm giá trị của x sao cho: Q(x) + P(x) + 5x2 – 2 = 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bằng cách đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của VietJack.

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập