Cho ABC, lấy M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:
a) AC = EB và AC // BE;
b) Trên AC lấy điểm I, trên EB lấy điểm K sao cho AI = EK;
Chứng minh ba điểm: I, M, K thẳng hàng.
c) Từ E kẻ EH BC (H BC). Giả sử K là trung điểm của BE và HK = 5 cm; HE = 6 cm. Tính độ dài đoạn thẳng BH.
Cho ABC, lấy M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:
a) AC = EB và AC // BE;
b) Trên AC lấy điểm I, trên EB lấy điểm K sao cho AI = EK;
Chứng minh ba điểm: I, M, K thẳng hàng.
c) Từ E kẻ EH BC (H BC). Giả sử K là trung điểm của BE và HK = 5 cm; HE = 6 cm. Tính độ dài đoạn thẳng BH.
Câu hỏi trong đề: Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
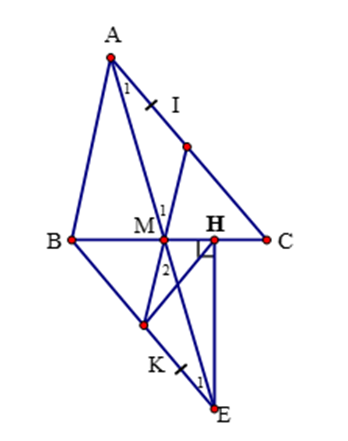
a) Xét tam giác AMC và tam giác EMB có:
MA = ME (GT)
(Hai góc đối đỉnh)
MC = MB (M là trung điểm của BC)
Do đó: tam giác AMC = tam giác EMB (c – g – c)
=> AC = EB (Hai cạnh tương ứng) (1 điểm)
và (Hai góc tương ứng)
Mà và ở vị trí so le trong nên AC // BEXét AMI và EMK có:
AI = EK (GT)
(CM ở câu a)
MA = ME (GT)
Do đó: AMI = EMK (c – g – c)
=> (hai góc tương ứng)
Ta có: = 1800 (Hai góc kề bù) nên = 1800
Ba điểm I, M, K thẳng hàng.Vì BHE vuông tại H có HK là đường trung tuyến (do K là trung điểm của BE)
Nên HK =
BE = 2HK = 2.5 = 10 cm.
Áp dụng định lý Pytago vào tam giác BHE vuông tại H có:
BE2 = BH2 + HE2
102 = BH2 + 62
=> BH2 = 100 – 36 = 64
=> BH = 8 cmĐăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Vì n có hai chữ số nên 10 n 99 20 2n 198 21 2n + 1 199.
Vì 2n + 1 là số chính phương mà 21 2n + 1 199 nên 2n + 1 {25; 36; 49; 64; 81; 100; 121; 144; 169; 196}.
Vì 2n + 1 lẻ nên 2n + 1 {25; 49; 81; 121; 169} n {12; 24; 40; 60; 84} (1)
Vì 3n + 1 cũng là một số chính phương nên từ (1) n = 40.Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến:
P(x) = 2x4 + 9x2 – 3x + 7 – x – 4x2 – 2x4
P(x) = (2x4 – 2x4) + (9x2 – 4x2) + (–3x – x) + 7
P(x) = 5x2 – 4x + 7 (0,5 điểm)
Q(x) = – 5x3 – 3x – 3 + 7x – x2 – 2
Q(x) = – 5x3 – x2 + (–3x + 7x) + (–3 – 2)
Q(x) = – 5x3 – x 2 + 4x – 5 (0,5 điểm)
Bậc của đa thức P(x) là 2, bậc của đa thức Q(x) là 3 (0,5 điểm)
b) Ta có:
+) P(x) = 5x2 – 4x + 7
Thay vào đa thức P(x) ta được:
=
c,
|
+ |
Q(x) = – 5x3 – x 2 + 4x – 5 |
|
P(x) = 5x2 – 4x + 7 |
Q(x) + P(x) = – 5x3 + 4x2 + 2 (0,25 điểm)
|
– |
Q(x) = – 5x3 – x 2 + 4x – 5 |
|
P(x) = 5x2 – 4x + 7 |
Ta có: Q(x) + P(x) + 5x2 – 2 = 0
(–5x3 + 4x2 + 2) + 5x2 – 2 = 0
–5x3 + 9x2 = 0
x2(–5x + 9) = 0
Vậy x = 0 hoặc x = .
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập