Câu hỏi:
29/06/2022 648
Cho nửa đường tròn (O) đường kính AB. Kẻ tiếp tuyến Bx với nửa đường tròn. Gọi C là điểm trên nửa đường tròn sao cho cung CB bằng cung CA, D là một điểm tùy ý trên cung CB (D khác C và B). Các tia AC, AD cắt Bx theo thứ tự tại E và F.
a. Chứng minh rằng: ∆ABE là tam giác cân
b. Chứng minh rằng: FB2 = FD.FA
c. Chứng minh rằng: CDFE là tứ giác nội tiếp
Cho nửa đường tròn (O) đường kính AB. Kẻ tiếp tuyến Bx với nửa đường tròn. Gọi C là điểm trên nửa đường tròn sao cho cung CB bằng cung CA, D là một điểm tùy ý trên cung CB (D khác C và B). Các tia AC, AD cắt Bx theo thứ tự tại E và F.
a. Chứng minh rằng: ∆ABE là tam giác cân
b. Chứng minh rằng: FB2 = FD.FA
c. Chứng minh rằng: CDFE là tứ giác nội tiếp
Quảng cáo
Trả lời:
Giải bởi Vietjack
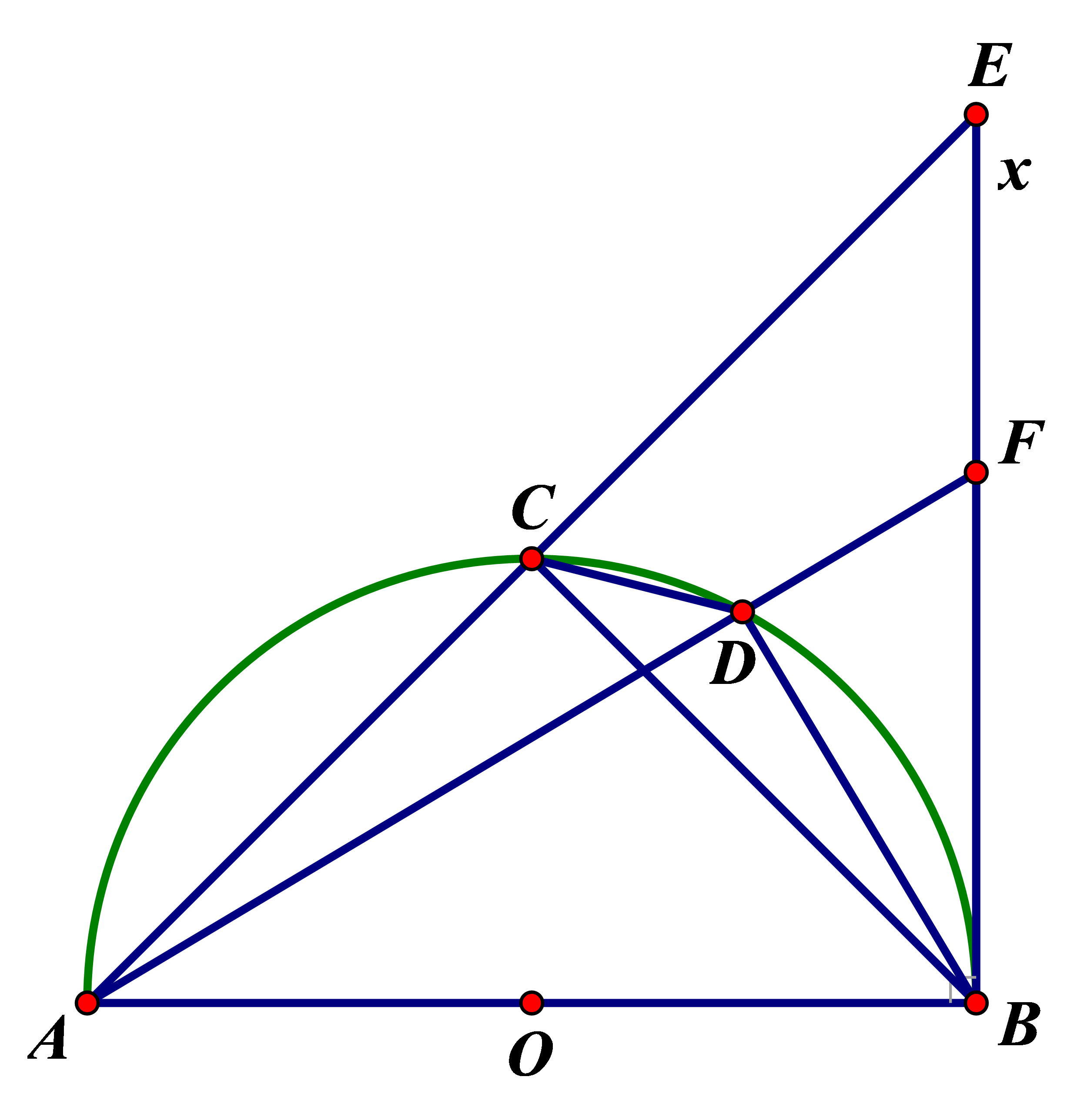
a. Ta có (hai góc nội tiếp chắn hai cung bằng nhau)
Ta lại có = 90° (góc nội tiếp chắn nửa đường tròn)
Suy ra tam giác CAB là tam giác vuông cân và = 45°
Xét tam giác ABE vuông tại B (Bx là tiếp tuyến của (O)) có = 45°
Dẫn đến = 180° − = 180 – 90 – 45 = 45° =
Suy ra tam giác ABE là tam giác vuông cân.
b. Xét ∆ FDB và ∆ FBA có:
là góc chung
= = 90° ( là góc nội tiếp chắn nữa đường tròn và Bx là tiếp tuyến của (O))
Suy ra ∆ FDB 
∆ FBA (g.g)
Từ đó suy ra FB2 = FD.FA (đpcm)
c. Từ câu b ta suy ra được: Trong một tam giác vuông thì bình phương cạnh góc vuông bằng tích hình chiếu của nó trên cạnh huyền nhân với cạnh huyền.
Xét tam giác ABF vuông tại B đường cao BD ta có: AB2 = AD.AF
ABE vuông tại B đường cao BC ta có: AB2 = AC.AE
Suy ra AD.AF = AC.AE
Xét ∆ ACD và ∆ AFE có:
là góc chung
(chứng minh trên)
Suy ra ∆ ACD ∆ AFE (c.g.c)
Suy ra suy ra tứ giác CDFE là tứ giác nội tiếp.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a. Vẽ (P)
Bảng giá trị:
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y = x2 |
4 |
1 |
0 |
1 |
4 |
Trên mặt phẳng tọa độ lấy các điểm A(−2; 4); B(−1; 1); O(0; 0); C(1; 1); D(2; 4).
Vẽ (d)
Đường thẳng (d): y = 2x + 3 có a = 2, b = 3 đi qua hai điểm (0; b) và
Do đó, hai điểm thuộc đường thẳng (d) là M(0; 3) và N(−1,5; 0).
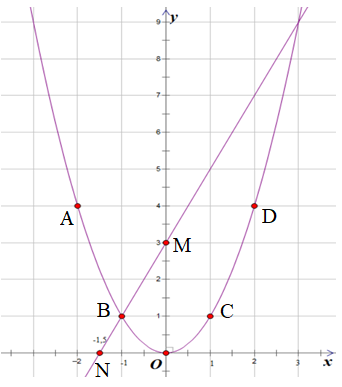
b. Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = 2x + 3
Û x2 – 2x – 3 = 0
Û x2 – 3x + x – 3 = 0
Û x(x – 3) + (x – 3) = 0
Û (x – 3)(x + 1) = 0
Û
• Với x = 3 thì y = 2x + 3 = 2.3 + 3= 9.
Do đó, ta có tọa độ giao điểm của (P) và (d) là A(3; 9).
• Với x = −1 thì y = 2x + 3 = 2.(−1) + 3 = 1.
Do đó, ta có tọa độ giao điểm của (P) và (d) là B(−1; 1).
Vậy hai đồ thị hàm số trên có hai giao điểm là A(3; 9) và B(−1; 1).
Lời giải
Gọi x (m) là chiều dài của khu vườn (x > 0)
y (m) là chiều rộng của khu vườn (y > 3)
Khu vườn hình chữ nhật có chu vi bằng 46m ta có: 2x + 2y = 46 (m) (1)
Chiều dài hình chữ nhật sau khi tăng 5 m là: x + 5 (m)
Chiều rộng hình chữ nhật sai khi giảm là: y – 3 (m)
Tăng chiều dài 5m và giảm chiều rông 3m thì chiều dài gấp 4 lần chiều rộng nên ta có phương trình: x + 5 = 4(y – 3) (2)
Từ (1) và (2), ta có hệ phương trình:
Û
Û
Û
Û (thỏa mãn)
Khi đó diện tích khu vườn là S = x.y = 15.8 = 120 (m2).
Vậy diện tích khu vườn hình chữ nhật là 120 m2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải