Câu hỏi:
11/07/2024 1,366
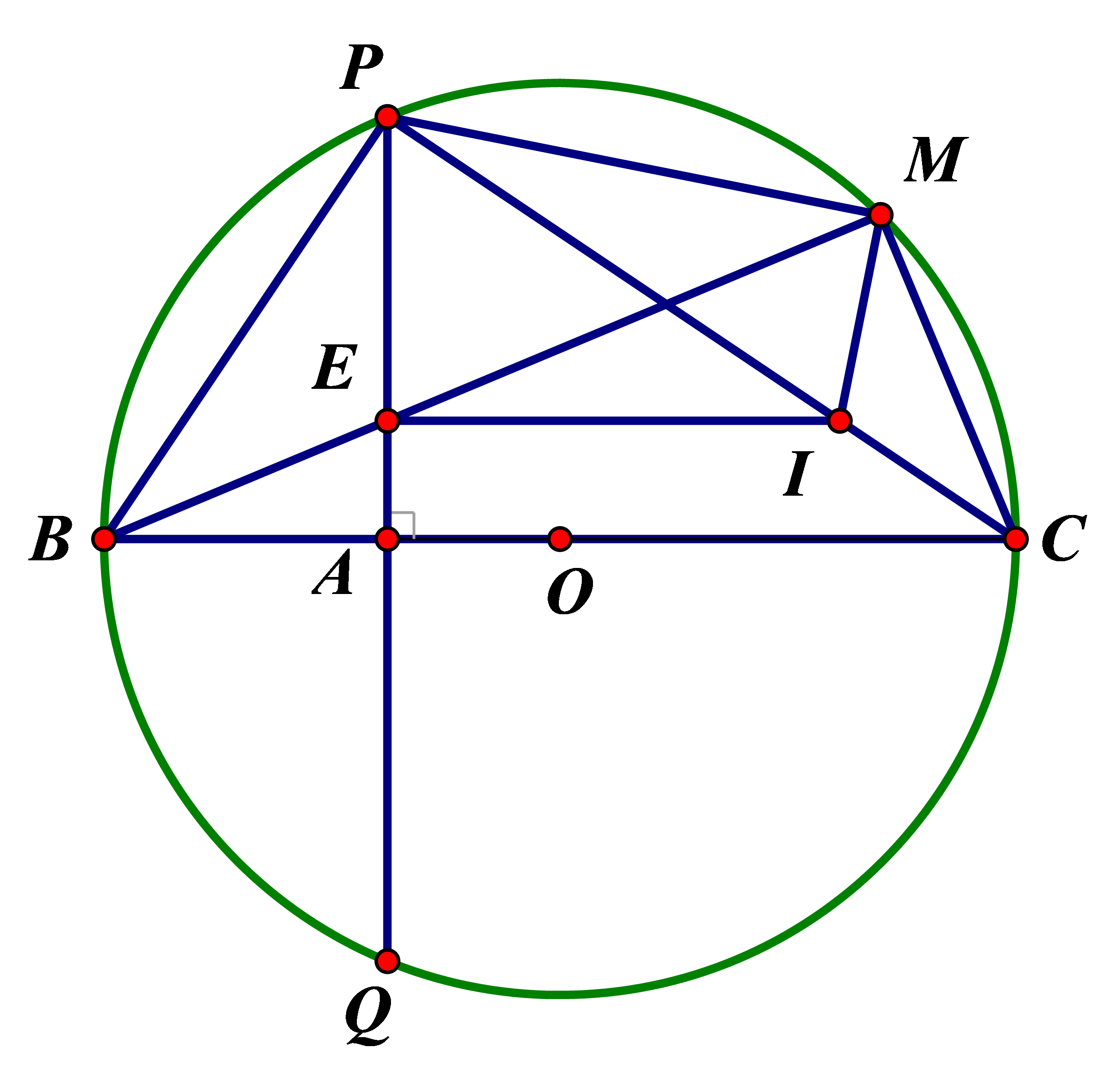
Cho đường tròn (O; R), đường kính BC cố định và điểm A cố định thuộc đoạn thẳng OB (A không trùng với O và B). Kẻ dây PQ ⊥ BC tại A. Lấy M thuộc cung lớn PQ (M không trùng với C). Nối BM cắt PQ tại E. Chứng minh:
a. Tứ giác AEMC nội tiếp
b. BP2 = BE. BM = BA.BC
c. Từ E kẻ đường thẳng song song BC cắt PC tại I. Chứng minh: và tâm đường tròn ngoại tiếp tam giác EPM nằm trên một đường thẳng cố định khi M di chuyển trên cung lớn PQ.
Cho đường tròn (O; R), đường kính BC cố định và điểm A cố định thuộc đoạn thẳng OB (A không trùng với O và B). Kẻ dây PQ ⊥ BC tại A. Lấy M thuộc cung lớn PQ (M không trùng với C). Nối BM cắt PQ tại E. Chứng minh:
a. Tứ giác AEMC nội tiếp
b. BP2 = BE. BM = BA.BC
c. Từ E kẻ đường thẳng song song BC cắt PC tại I. Chứng minh: và tâm đường tròn ngoại tiếp tam giác EPM nằm trên một đường thẳng cố định khi M di chuyển trên cung lớn PQ.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a. = 90° (EA vuông góc AC)
= 90° (Góc nội tiếp chắn nửa đường tròn)
Xét tứ giác ABOC có + = 90° + 90° = 180°
Suy ra tứ giác AEMC nội tiếp (đpcm).
b. Xét ∆ BAP và ∆ BPC có:
là góc chung
= 90° ( là góc nội tiếp chắn nửa đường tròn)
Suy ra ∆ BAP ∆ BPC (g.g)
Từ đó suy ra (1)
Xét ∆ BEA và ∆ BCM có:
là góc chung
(tứ giác AEMC nội tiếp)
Suy ra ∆ BEA đồng dạng ∆ BCM (g.g)
Từ đó suy ra (2)
Từ (1) và (2) suy ra: BP2 = BE. BM = BA.BC (đpcm)
c. Ta có:
(hai góc đồng vị).
(tứ giác PMCB nội tiếp đường tròn O).
Suy ra .
Tứ giác EPMI có suy ra tứ giác EPMI nội tiếp.
Ta có: = 90°
Ta có tâm đường tròn ngoại tiếp tam giác EPM cũng là tâm của đường tròn ngoại tiếp tứ giác EPMI.
Mà ta có = 90° dẫn đến PI là đường kính .
Suy ra tâm của đường tròn ngoại tiếp tam giác EPM là trung điểm của PI.
Mà điểm này cũng thuộc đường thẳng PC với P và C cố định nên ta suy ra điều phải chứng minh.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) x2 + 3x – 4 = 0
Û x2 + 4x – x – 4 = 0
Û x(x + 4) – (x + 4) = 0
Û (x – 1)(x + 4) = 0
Û
Vậy phương trình có tập nghiệm là S = {1; −4}.
b) Điều kiện xác định y – 1 > 0 Û y > 1.
Đặt t = (t > 0) (vì y > 1 nên , do đó )
Ta có hệ phương trình:
Û
Û
Û
Û (thỏa mãn)
Suy ra = 1 Û = 1
Û y – 1 = 1 Û y = 2 (thỏa mãn)
Vậy hệ phương trình đã cho có nghiệm là (2; 2).
Lời giải
a. Với m = 1 phương trình trở thành: x2 – 4x + 1 = 0
Tính ∆ = b2 – 4ac. Phương trình có các hệ số là a = 1; b = −4; c = 1.
∆ = (−4)2 – 4.1.1 = 16 – 4 = 12 > 0.
Do ∆ > 0, áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt:
x1 = ; x2 = .
Vậy phương trình có tập nghiệm là S = .
b. ∆’ = (b’)2 – ac = (−m – 1)2 – m2.1 = m2 + 2m + 1 – m2 = 2m + 1
Để phương trình có 2 nghiệm phân biệt thì:
∆’ > 0 Û 2m + 1 > 0 Û m > .
Vậy giá trị m nguyên nhỏ nhất để phương trình (1) có hai nghiệm phân biệt là m = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận