Cho phương trình x2 – 2(m − 3)x + 4m – 16 = 0 (m là tham số)
a) Tìm m để phương trình có nghiệm x = 3. Giải phương trình với giá trị m vừa tìm được.
b) Chứng minh rằng phương trình luôn có nghiệm với mọi m.
c) Tìm m để phương trình có ít nhất một nghiệm âm.
Cho phương trình x2 – 2(m − 3)x + 4m – 16 = 0 (m là tham số)
a) Tìm m để phương trình có nghiệm x = 3. Giải phương trình với giá trị m vừa tìm được.
b) Chứng minh rằng phương trình luôn có nghiệm với mọi m.
c) Tìm m để phương trình có ít nhất một nghiệm âm.
Câu hỏi trong đề: Đề kiểm tra giữa học kì 2 môn Toán 9 có đáp án (Mới nhất) !!
Quảng cáo
Trả lời:
a) Thay x = 3 vào phương trình đã cho ta được
32 – 2(m – 3).3 + 4m – 16 = 0
9 – 6m + 18 + 4m −16 = 0
11 – 2m = 0
Khi phương trình trở thành
x2 – 2.x + 4.![]() – 16 = 0
– 16 = 0
x2 – 5x + 6 = 0
x2 – 2x – 3x + 6 = 0
x(x – 2) −3(x – 2) = 0
(x – 2)(x – 3) = 0
Vậy phương trình có tập nghiệm là S = {2; 3}.
b) Ta có: ∆’ = [– (m – 3)]2 – 1.(4m – 16)
= m2 – 6m + 9 − 4m + 16
= m2 −10m + 25 = (m – 5)2.
Vì ∆’ = (m – 5)2 ≥ 0 (đúng với mọi giá trị của m).
Nên phương trình luôn có nghiệm (điều phải chứng minh).
c) Do phương trình luôn có nghiệm, áp dụng định lý Vi-et, ta được:
Trường hợp 1: Phương trình có 1 nghiệm x1 = 0 và một nghiệm âm. Khi đó:
x1.x2 = 0 tương đương 4m – 16 = 0 Û m = 4
Do đó x1 + x2 = x2 = 2m – 6 = 2 (không thỏa mãn)
Trường hợp 2: Phương trình có một nghiệm âm và một nghiệm dương. Khi đó:
x1.x2 < 0 Û 4m – 16 < 0 Û m < 4
Trường hợp 3: Phương trình có hai nghiệm âm. Khi đó:
(không tồn tại giá trị m)
Vậy để phương trình có ít nhất một nghiệm âm thì m < 4.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
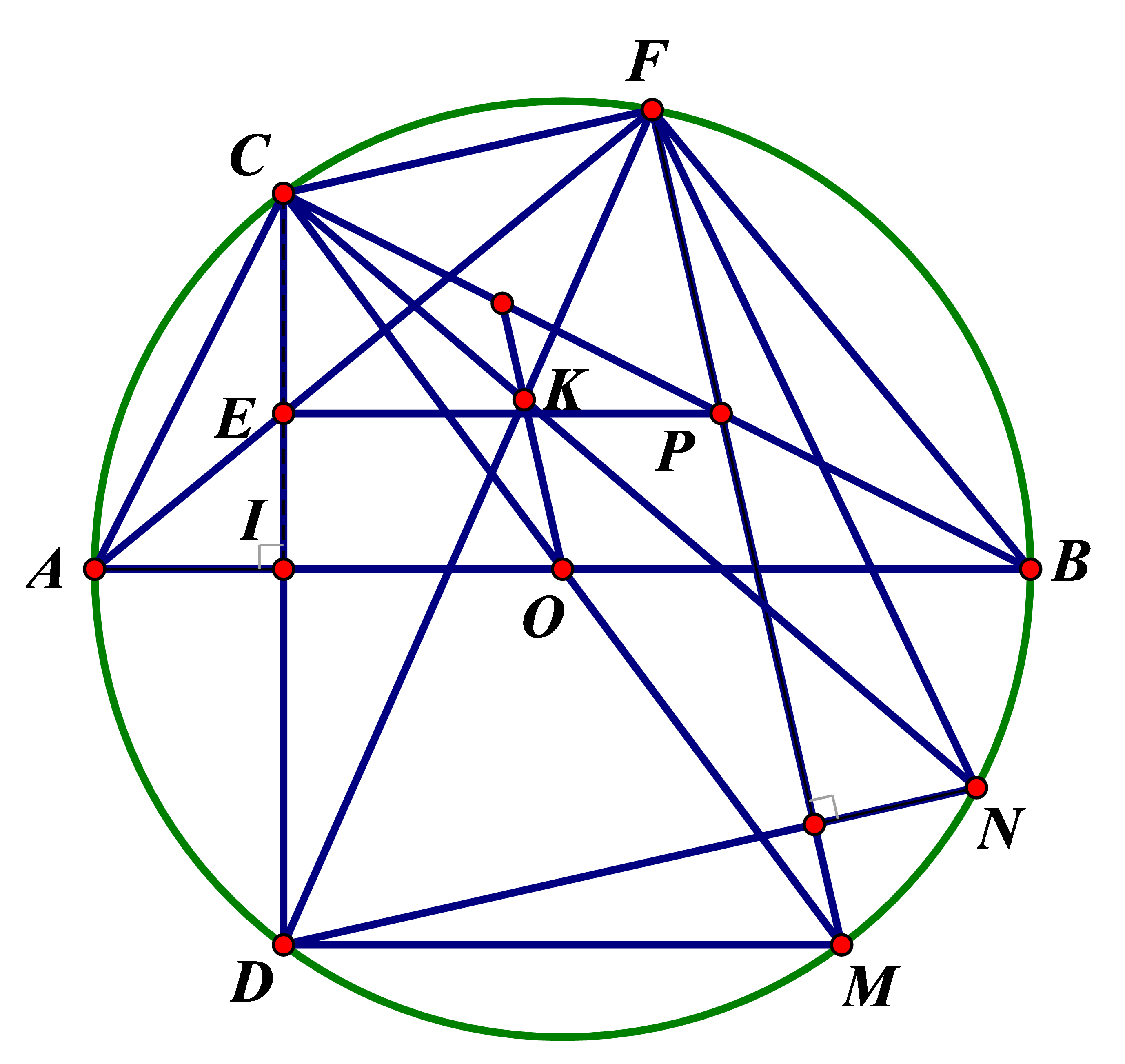
a) Ta có: = 90° (vì CI ⊥ AB)
= 90° (góc nội tiếp chắn nửa đường tròn)
Xét tứ giác BIEF có += 90° + 90° = 180°
Suy ra tứ giác BIEF nội tiếp.
b) Tam giác ABC có = 90° (góc nội tiếp chắn nửa đường tròn)
Suy ra ∆ACB vuông tại C
Xét ∆ACB vuông tại C đường cao IC, ta được:
AC2 = AI . AB (1)
Xét ∆ AEI và ∆ ABF có:
là góc chung
(tứ giác BIEF nội tiếp)
Suy ra ∆ AEI ![]() ∆ ABF (g.g)
∆ ABF (g.g)
Từ đó suy ra (2)
Từ (1) và (2) suy ra
AC2 = AI.AB = AE.AF (điều phải chứng minh)
c) Ta có CF ⊥ FM ( = 90° góc nội tiếp chắn nửa đường tròn)
DN ⊥ FM (giả thiết)
Suy ra CF // DM
Suy ra tứ giác CFND là hình thang (3)
Ta có (hai góc so le trong của CF // DN)
Suy ra (hai góc nội tiếp bằng nhau)
Û
Û
(hai góc nội tiếp chắn hai cung bằng nhau) (4)
Từ (3) và (4) suy ra tứ giác CFND là hình thang cân.
Suy ra CN = FD (hai đường chéo của hình thang cân).
d) Ta có K là giao điểm của CN và FD nên:
CK = KF
Mà ta cũng có CO = OF = R.
Suy ra OK là trung trực của CF.
Suy ra tâm đường tròn ngoại tiếp của CEF sẽ thuộc đường thẳng OK (5)
Ta có O là trung điểm CM.
I là trung điểm CD (đường kính vuông góc với dây thì đi qua trung điểm của dây).
Suy ra OI là đường trung bình của ∆DCM.
Suy ra IO // DM.
Suy ra AB // DM.
Đường tròn (O) có dây AB // dây DM suy ra
Gọi P là giao điểm của FM và CB.
Xét tứ giác ECFP có
Suy ra tứ giác ECFP nội tiếp.
Tứ giác ECFP nội tiếp có = 90° (góc nội tiếp chắn nửa đường tròn)
Suy ra CP là đường kính của đường tròn ngoại tiếp tứ giác ECFP.
Suy ra tâm đường tròn ngoại tiếp tứ giác ECFP thuộc CP.
Hay tâm đường tròn ngoại tiếp tam giác CEF thuộc CB (6)
Từ (5) và (6) suy ra tâm đường tròn ngoại tiếp ∆CEF là giao điểm của OK và BC
Lời giải
Gọi x (công việc) là phần công việc tổ 1 làm được trong 1 giờ (x > 0).
Gọi y (công việc) là phần công việc tổ 2 làm được trong 1 giờ (y > 0).
3 giờ 36 phút = 3,6 giờ.
Nếu cả hai tổ cùng làm thì sau 3 giờ 36 phút giờ sẽ xong nên
3,6x + 3,6y = 1 (1)
Nếu tổ 1 làm trong 2 giờ, tổ 2 làm trong 3 giờ thì được ![]() công việc nên
công việc nên
2x + 3y = ![]() (2)
(2)
Từ (1) và (2) ta có hệ phương trình
(thỏa mãn)
Ta có:
Tổ 1 mỗi giờ làm được ![]() công việc nên một mình tổ 1 sẽ hoàn thành công việc trong 6 giờ.
công việc nên một mình tổ 1 sẽ hoàn thành công việc trong 6 giờ.
Tổ 2 mỗi giờ làm được công việc nên một mình tổ 2 sẽ hoàn thành công việc trong 9 giờ.
Vậy tổ 1 làm một mình thì xong công việc trong 6 giờ, tổ 2 làm một mình thì xong công việc trong 9 giờ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.