Câu hỏi:

13/07/2024 19,968

Cho đường tròn tâm O đường kính AB. Dây CD vuông góc với AB tại E (E nằm giữa A và O; E không trùng A, không trùng O). Lấy điểm M thuộc cung nhỏ BC sao cho cung MB nhỏ hơn cung MC. Dây AM cắt CD tại F. Tia BM cắt đường thẳng CD tại K.

1) Chứng minh tứ giác BMFE nội tiếp.

2) Chứng minh BF vuông góc với AK và EK.EF = EA.EB

3) Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra giữa học kì 2 môn Toán 9 có đáp án (Mới nhất) !!

Sách mới 2k7: Bộ 20 đề minh họa Toán, Lí, Hóa, Văn, Sử, Địa…. form chuẩn 2025 của Bộ giáo dục (chỉ từ 110k).

20 đề Toán 20 đề Văn Các môn khác

Quảng cáo

Trả lời:

Giải bởi Vietjack

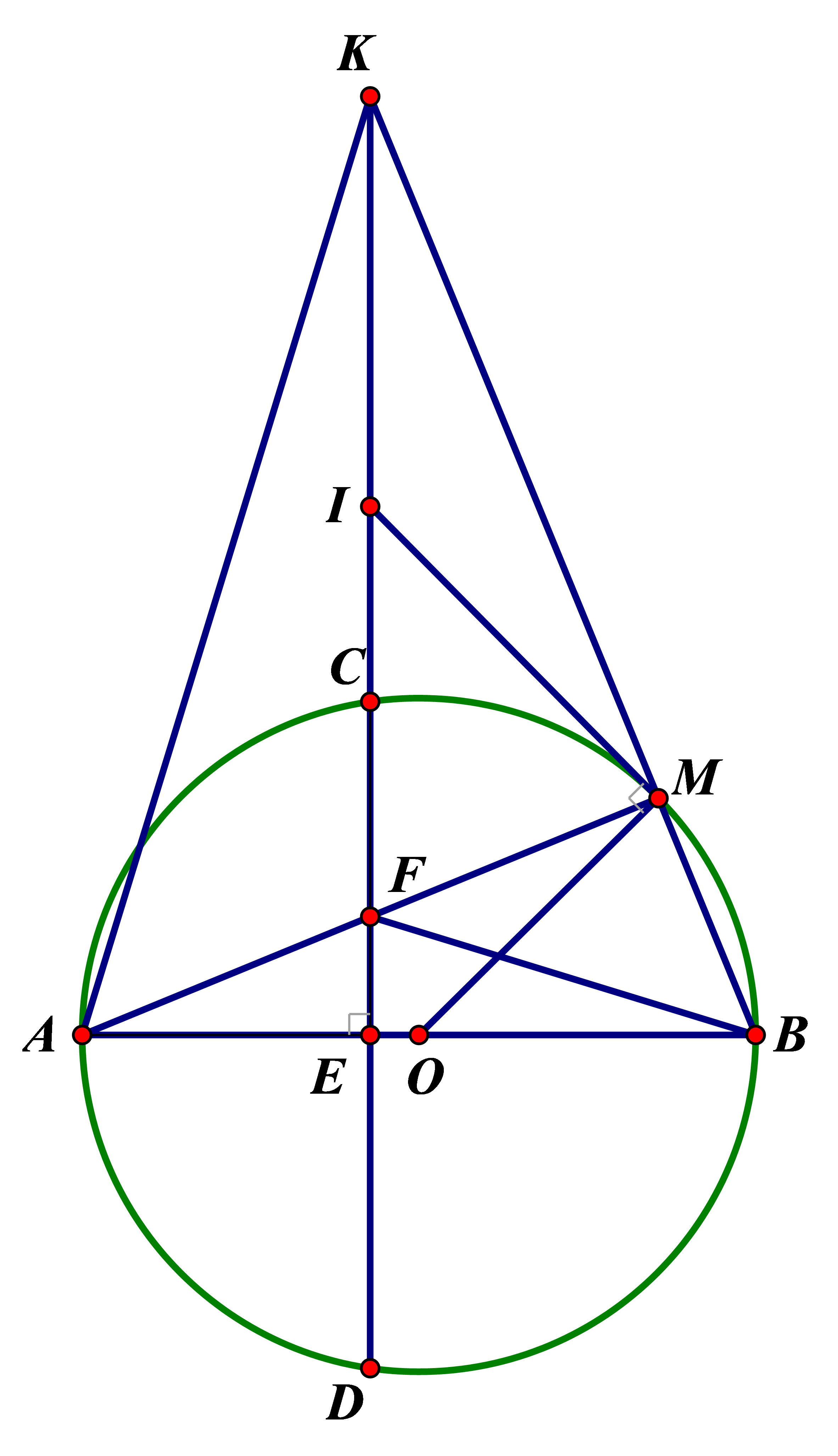
Cho đường tròn tâm O đường kính AB. Dây CD vuông góc với AB tại E (E nằm giữa A và O; E không trùng A, không trùng O). Lấy điểm M thuộc cung nhỏ BC sao cho cung MB nhỏ hơn cung MC. Dây AM cắt CD tại F. Tia BM cắt đường thẳng CD tại K. 1) Chứng minh tứ giác BMFE nội tiếp. 2) Chứng minh BF vuông góc với AK và EK.EF = EA.EB 3) Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF. (ảnh 1)

1) Ta có: $\hat{F E B}$ = 90° (CE ⊥ AB)

$\hat{F M B}$ = 90° (góc nội tiếp chắn nửa đường tròn)

Xét tứ giác BMFE có $\hat{F E B}$ + $\hat{F M B}$ = 90° + 90° = 180°

Suy ra tứ giác BMFE nội tiếp.

2) Ta có $\hat{A M B}$ = 90° (góc nội tiếp chắn nửa đường tròn)

Suy ra AM ⊥ MB

Xét tam giác AKB có:

KE ⊥ AB (giả thiết)

AM ⊥ KB (chứng minh trên)

Mà KE cắt AM tại F suy ra F là trực tâm của ∆AKB.

Suy ra BF ⊥ AK.

Xét ∆ AFE và ∆ KBE có:

$\hat{A E F} = \hat{K E B}$ = 90° (KE ⊥ AB)

$\hat{A F E} = \hat{K B E}$ (tứ giác BMFE nội tiếp)

Suy ra ∆AFE ∆KBE (g.g)

Từ đó suy ra $\frac{A E}{K E} = \frac{F E}{B E} \Leftrightarrow A E . B E = K E . E F$ (điều phải chứng minh)

3) Xét tam giác AOM có:

OA = OM = R suy ra ∆AOM cân tại O suy ra $\hat{O M A} = \hat{O A M}$ (1)

Ta có $\hat{A M O} + \hat{I M F} = \hat{I M O} = 90 ° \hat{A M O} + \hat{I M F} = \hat{I M O} = 90 °$ (MI là tiếp tuyến của (O))

$\hat{K M I} + \hat{I M F} = \hat{K M F} = 90 °$ (KM ⊥ FM)

Suy ra $\hat{A M O} = \hat{K M I}$ (2)

Mà ∆AFE ∆KBE suy ra $\hat{O A M} = \hat{I K M}$ (hai góc tương ứng) (3)

Từ (1) (2) và (3) suy ra $\hat{I M K} = \hat{I K M}$

Suy ra tam giác IMK cân tại I suy ra IM = IK (4)

Xét ∆KMF vuông tại M ta có:

$\hat{F K M} + \hat{K F M} = 90 °$

$\hat{K M I} + \hat{I M F} = 90 °$

Mà $\hat{I M K} = \hat{I K M}$ (chứng minh trên)

Nên $\hat{I M F} = \hat{I F M}$ suy ra ∆IMF cân tại I suy ra IM = IF (5)

Từ (4) và (5) suy ra KI = IF (= IM) (điều phải chứng minh)

Nhà sách VIETJACK:

Xem thêm kho sách »

Combo - Sổ tay kiên thức trọng tâm Toán, Lí, Hóa dành cho 2k7 VietJack

₫29.000 (Đã bán 152)

Sách - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 cho 2k7 VietJack

₫140.000 ₫300.000 (Đã bán 1,2k)

Sách Combo - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) - 2025 cho 2k7 VietJack

₫140.000 ₫300.000 (Đã bán 1,6k)

Sách - Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 cho 2k7 VietJack

₫140.000 ₫300.000 (Đã bán 2,7k)

Bình luận hoặc Báo cáo
về câu hỏi!

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Một khu vườn hình chữ nhật có chu vi bằng 68 m. Nếu tăng chiều rộng lên gấp đôi và chiều dài lên gấp ba thì chu vi khu vườn mới là 178 m. Hãy tìm chiều dài, chiều rộng của khu vườn đã cho lúc ban đầu.

Xem đáp án » 13/07/2024 6,606

Câu 2:

Cho hệ phương trình: ${\begin{cases} 2 x + y = 3 m - 2 \\ 3 x - y = 2 m + 2 \end{cases}$ (m là tham số) (I)

1) Giải hệ phương trình đã cho khi m = −1.

2) Tìm m để hệ (I) có cặp nghiệm (x; y) duy nhất thỏa mãn: x² + y² = 10.

Xem đáp án » 13/07/2024 2,464

Câu 3:

Cho x, y là hai số thực thỏa mãn x.y = 1.

Chứng minh rằng $\frac{4}{{(x + y)}^{2}} + x^{2} + y^{2} \geq 3$ . Đẳng thức xảy ra khi nào?

Xem đáp án » 13/07/2024 1,575

Câu 4:

Cho $P = (\frac{1}{\sqrt{x} + 1} - \frac{1}{x + \sqrt{x}}) : \frac{\sqrt{x}}{x + 2 \sqrt{x} + 1}$ (với x > 0)

1) Rút gọn biểu thức P.

2) Tính giá trị của P khi x = 4.

3) Tìm giá trị của x để $P > \frac{2}{3}$ .

Xem đáp án » 12/07/2024 506

Xem thêm các câu hỏi khác »

Bình luận

Hỏi bài tập

🔥 Đề thi HOT:

Đăng ký gói thi VIP

VIP +3 tháng ( 199,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +6 tháng ( 299,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Siêu tiết kiệm - Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

Nhà sách VIETJACK:

Một khu vườn hình chữ nhật có chu vi bằng 68 m. Nếu tăng chiều rộng lên gấp đôi và chiều dài lên gấp ba thì chu vi khu vườn mới là 178 m. Hãy tìm chiều dài, chiều rộng của khu vườn đã cho lúc ban đầu.

Cho hệ phương trình: {2x+y=3m−23x−y=2m+2 (m là tham số) (I) 1) Giải hệ phương trình đã cho khi m = −1. 2) Tìm m để hệ (I) có cặp nghiệm (x; y) duy nhất thỏa mãn: x2 + y2 = 10.

Cho x, y là hai số thực thỏa mãn x.y = 1. Chứng minh rằng 4(x+y)2+x2+y2≥3. Đẳng thức xảy ra khi nào?

Cho P=(1x+1−1x+x):xx+2x+1 (với x > 0) 1) Rút gọn biểu thức P. 2) Tính giá trị của P khi x = 4. 3) Tìm giá trị của x để P>23.

Bình luận

🔥 Đề thi HOT:

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hệ phương trình: ${\begin{cases} 2 x + y = 3 m - 2 \\ 3 x - y = 2 m + 2 \end{cases}$ (m là tham số) (I)

1) Giải hệ phương trình đã cho khi m = −1.

2) Tìm m để hệ (I) có cặp nghiệm (x; y) duy nhất thỏa mãn: x² + y² = 10.

Cho x, y là hai số thực thỏa mãn x.y = 1.

Chứng minh rằng $\frac{4}{{(x + y)}^{2}} + x^{2} + y^{2} \geq 3$ . Đẳng thức xảy ra khi nào?

Cho $P = (\frac{1}{\sqrt{x} + 1} - \frac{1}{x + \sqrt{x}}) : \frac{\sqrt{x}}{x + 2 \sqrt{x} + 1}$ (với x > 0)

1) Rút gọn biểu thức P.

2) Tính giá trị của P khi x = 4.

3) Tìm giá trị của x để $P > \frac{2}{3}$ .