Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 10
27 người thi tuần này 4.6 21.4 K lượt thi 5 câu hỏi 90 phút
- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
1)
2) Khi x = 4
3) Ta có:
do x > 0 nhân 2 vế cho 3x ta được
3(x – 1) > 2x
Vậy khi x > 3 thì .
Lời giải
Gọi x (m) là chiều rộng của khi vườn lúc đầu (x > 0).
Gọi y (m) là chiều rộng của khi vườn lúc đầu (y > 0).
Khu vườn lúc đầu có chu vi bằng 68 m nên 2x + 2y = 68 (1)
Chiều rộng khu vườn sau khi tăng là 2x (m)
Chiều dài khu vườn sau khi tăng là 3y (m)
Chu vi của khu vườn sau khi tăng là 2.2x + 2.3y = 178 (2)
Từ (1) và (2) ta có hệ phương trình:
(thỏa mãn)
Vậy chiều rộng lúc ban đầu là 13 m và chiều dài lúc ban đầu là 21 m.
Lời giải
Ta có nên hệ phương trình luôn có cặp nghiệm (x; y) duy nhất.
1) Khi m = −1 thì (I)
Vậy phương trình có cặp nghiệm là (−1; −3).
2) Thay vào biểu thức x2 + y2 = 10 ta được:
m2 + (m – 2)2 = 10
m2 + m2 − 4m + 4 =10
2m2 − 4m − 6 = 0
m2 − 2m – 3 = 0
m2 − 3m + m – 3 = 0
m(m − 3) + m − 3 = 0
(m + 1)(m – 3) = 0
Vậy m = −1 hoặc m = 3 thì hệ (I) có cặp nghiệm (x; y) duy nhất thỏa mãn: x2 + y2 = 10.
Lời giải
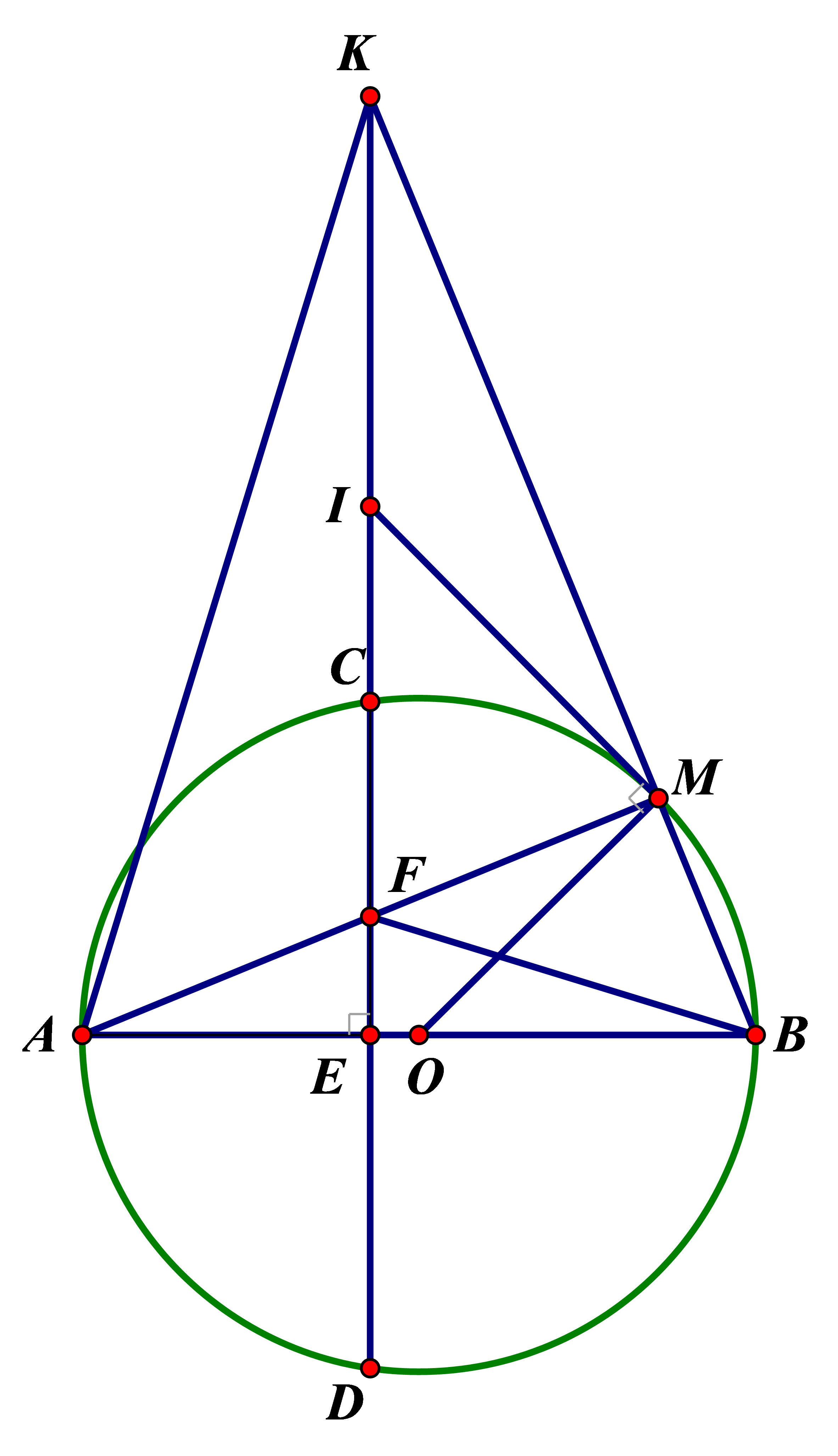
1) Ta có: = 90° (CE ⊥ AB)
= 90° (góc nội tiếp chắn nửa đường tròn)
Xét tứ giác BMFE có += 90° + 90° = 180°
Suy ra tứ giác BMFE nội tiếp.
2) Ta có = 90° (góc nội tiếp chắn nửa đường tròn)
Suy ra AM ⊥ MB
Xét tam giác AKB có:
KE ⊥ AB (giả thiết)
AM ⊥ KB (chứng minh trên)
Mà KE cắt AM tại F suy ra F là trực tâm của ∆AKB.
Suy ra BF ⊥ AK.
Xét ∆ AFE và ∆ KBE có:
= 90° (KE ⊥ AB)
(tứ giác BMFE nội tiếp)
Suy ra ∆AFE ![]() ∆KBE (g.g)
∆KBE (g.g)
Từ đó suy ra (điều phải chứng minh)
3) Xét tam giác AOM có:
OA = OM = R suy ra ∆AOM cân tại O suy ra (1)
Ta có (MI là tiếp tuyến của (O))
(KM ⊥ FM)
Suy ra (2)
Mà ∆AFE ![]() ∆KBE suy ra (hai góc tương ứng) (3)
∆KBE suy ra (hai góc tương ứng) (3)
Từ (1) (2) và (3) suy ra
Suy ra tam giác IMK cân tại I suy ra IM = IK (4)
Xét ∆KMF vuông tại M ta có:
Mà (chứng minh trên)
Nên suy ra ∆IMF cân tại I suy ra IM = IF (5)
Từ (4) và (5) suy ra KI = IF (= IM) (điều phải chứng minh)
Lời giải
Gọi A =
Áp dụng bất đẳng thức Cô-si:
(điều phải chứng minh)
Dấu “=” xảy ra khi x = y = 1.
Vậy đẳng thức xảy ra khi x = y = 1.