Biểu diễn các số hữu tỉ \( - \frac{1}{3};\,\,\frac{1}{6};\,\,1\) lần lượt bằng các điểm A, B, C trên trục số ở Hình 10.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 7 Bài tập cuối chương 1 có đáp án !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

Ta có: \( - \frac{1}{3} = \frac{{ - 2}}{6}\).

Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ).

Đi theo ngược chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 2 đơn vị mới đến điểm A. Điểm A biểu diễn số hữu tỉ \(\frac{{ - 2}}{6}\) hay \( - \frac{1}{3}\).

Đi theo chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 1 đơn vị mới đến điểm B. Điểm B biểu diễn số hữu tỉ \(\frac{1}{6}\).

Điểm C biểu diễn số hữu tỉ 1.

Ta biểu diễn các điểm A, B, C trên trục số như sau:

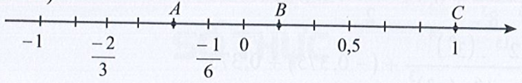
Media VietJack

Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Viện Hàn lâm Nhi khoa Mĩ (AAP) khuyến nghị, khối lượng cặp sách của học sinh tiểu học và trung học cơ sở không nên vượt quá 10% khối lượng cơ thể. Một nghiên cứu tại Tây Ban Nha cũng chỉ ra, học sinh mang cặp sách nặng trong thời gian dài sẽ tăng nguy cơ mắc các bệnh về cột sống. Những chiếc cặp quá nặng không chỉ gây cong vẹo cột sống, gù, mà còn ảnh hưởng tới phát triển chiều cao của trẻ.

(Nguồn: http://vnexpress.net/tac-hai-cua-viec-tre-cong-cap-di-hoc-4161875.html)

Bạn Đức học lớp 7 có cân nặng 46 kg. Hằng ngày, bạn Đức đi học mang một chiếc cặp sách nặng 3,5 kg. Hôm nay, bạn Đức cần đem thêm một số quyển vở mới, mỗi quyển vở nặng kg để tặng học sinh vùng lũ lụt. Bạn Đức có thể mang theo nhiều nhất bao nhiêu quyển vở để khối lượng cặp sách phù hợp với khuyến nghị trên?

Lời giải

Lời giải:

Theo khuyến nghị, khối lượng cặp sách bạn Đức nên mang không vượt quá là:

46 . 10% = 4,6 (kg).

Khối lượng bạn Đức có thể mang thêm nhiều nhất theo khuyến nghị là:

4,6 – 3,5 = 1,1 (kg).

Ta có: \(1,1:\frac{4}{{25}} = 1,1.\frac{{25}}{4} = 6,875\).

Do đó bạn Đức có thể mang theo nhiều nhất 6 quyển vở để khối lượng cặp sách phù hợp với khuyến nghị trên.

Câu 2

Tính một cách hợp lí:

\(\frac{{ - 5}}{7}\,\,.\,\,\frac{2}{{11}} + \frac{{ - 5}}{7}\,\,.\,\,\frac{9}{{11}} + \frac{5}{7}\);

Lời giải

Lời giải:

\(\frac{{ - 5}}{7}\,\,.\,\,\frac{2}{{11}} + \frac{{ - 5}}{7}\,\,.\,\,\frac{9}{{11}} + \frac{5}{7}\)

\( = \frac{{ - 5}}{7}\,\,.\,\,\left( {\frac{2}{{11}} + \frac{9}{{11}}} \right) + \frac{5}{7}\)

\( = \frac{{ - 5}}{7}\,\,.\,\,1 + \frac{5}{7} = \frac{{ - 5}}{7} + \frac{5}{7} = 0\);

Câu 3