Câu hỏi trong đề: Giải SBT Toán 10 Bài tập cuối chương 1 có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: C
Do y và x là các số tự nhiên, nên ta lần lượt thay các giá trị của x bởi 0, 1, 2,... để tìm y thỏa mãn.
Ta có:
Với x = 0 thì y = 5 – 02 = 5 ∈ ℕ;
Với x = 1 thì y = 5 – 12 = 4 ∈ ℕ;
Với x = 2 thì y = 5 – 22 = 1 ∈ ℕ;
Với x = 3 thì y = 5 – 32 = – 4 ∉ ℕ, không thỏa mãn, ta dừng lại.
Vậy các giá trị y thỏa mãn là 1, 4, 5.
Do đó, {y ∈ ℕ | y = 5 – x2, x ∈ ℕ} = {1; 4; 5}.
Các tập con của tập hợp {1; 4; 5} là ∅, {1}, {4}, {5}, {1; 4}, {1; 5}, {4; 5}, {1; 4; 5}.
Vậy có 8 tập con thỏa mãn.
Ngoài ra, ta có thể tính số tập con của một tập gồm k phần tử bằng cách tính 2k.
Tập {1; 4; 5} có 3 phần tử nên có 23 = 8 tập con.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Kí hiệu A là tập hợp các học sinh của lớp, B = {x ∈ A | x thích bóng rổ},
C = {x ∈ A | x thích bóng bàn}, D = {x ∈ A | x không thích môn nào trong hai môn}.
Theo giả thiết, ta có: n(A) = 36, n(B) = 20, n(C) = 14 và n(D) = 10.
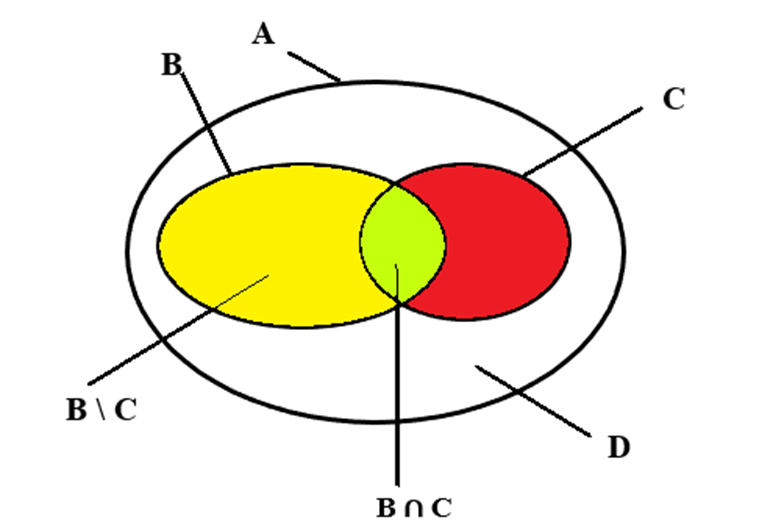
Số học sinh thích một trong hai môn là:
n(B ∪ C) = n(A) – n(D) = 36 – 10 = 26 (bạn).
Số học sinh thích cả hai môn thể thao trên là:
n(B ∩ C) = n(B) + n(C) – n(B ∪ C) = 20 + 14 – 26 = 8 (bạn).
Lời giải
Đáp án đúng là: B
Ta có {0} là một tập hợp, 0 là một phần tử nên viết 0 = {0} là sai, do đó đáp án A sai.
0 là một phần tử của tập hợp {0}, do đó ta viết 0 ∈ {0} là đúng nên đáp án B đúng.
Kí hiệu ⊂ dùng để chỉ mối quan hệ giữa các tập hợp nên đáp án C sai.
∅ là một tập hợp nên đáp án D sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.