Câu hỏi:
13/07/2024 14,532
Cho tam giác ABC có ba góc nhọn (AB < AC) có hai đường cao BE và CF cắt nhau tại H (E ∈ AC, F ∈ AB).
a) Chứng minh ∆ ABE ᔕ ∆ ACF.
b) Chứng minh ∆ AEF ᔕ ∆ ABC.
c) Vẽ AI ⊥ EF tại I. Qua C vẽ đường thẳng d vuông góc với AC. Đường thẳng AI và đường thẳng d cắt nhau tại K. Chứng minh AE.AC = AI. AK và BHCK là hình bình hành.
Cho tam giác ABC có ba góc nhọn (AB < AC) có hai đường cao BE và CF cắt nhau tại H (E ∈ AC, F ∈ AB).
a) Chứng minh ∆ ABE ᔕ ∆ ACF.
b) Chứng minh ∆ AEF ᔕ ∆ ABC.
c) Vẽ AI ⊥ EF tại I. Qua C vẽ đường thẳng d vuông góc với AC. Đường thẳng AI và đường thẳng d cắt nhau tại K. Chứng minh AE.AC = AI. AK và BHCK là hình bình hành.
Câu hỏi trong đề: Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Xét ∆ ABE và ∆ ACF có:
chung
= = 90° (Vì BE và CF lần lượt vuông góc với AC và AB)
Do đó ∆ ABE ᔕ ∆ ACF (g.g).
b) Ta có: ∆ABE ᔕ ∆ACF
=
=
Xét ∆ AEF và ∆ ABC có:
chung
= (cmt)
Do đó ∆ AEF ᔕ ∆ ABC (c.g.c).
c)
+ Xét ∆ AIE và ∆ ACK ta có:
chung
= = 90°
Do đó ∆ AIE ᔕ ∆ ACK (g.g).
=
AE.AC = AI. AK (đpcm)
+ Vì BE và CK cùng vuông góc với AC nên: BE // CK hay là BH // CK (1)
Ta có: = (cmt)
⇔ AE.AC = AF.AB
Mà AE.AC = AI. AK (cmt)
⇒ AF.AB = AI. AK
⇒
Xét ∆ AIF và ∆ ABK ta có:
(cmt)
chung
⇒ ∆ AIF ~ ∆ ABK (c – g – c)
⇒ (hai góc tương ứng)
⇒ BK ⊥ AB
Mà CF ⊥ AB
⇒ BK // CF (2)
Từ (1) và (2) suy ra BHCK là hình bình hành.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
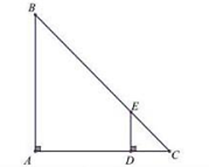
Hình vẽ minh họa
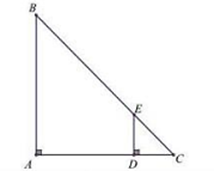
Xét ∆ABC và ∆DEC ta có:
chung
= = 90°
Do đó ∆ ABC ᔕ ∆ DEC (g.g)
=
AB = =
AB = 12m
Vậy độ cao của cây AB là 12m.
Lời giải
Theo đầu bài, khi mua hoa hồng vàng và mua nhiều hơn 10 bông hoa thì từ bông hoa thứ 11 trở đi, mỗi bông được giảm giá 2000 đồng nên số hoa hồng vàng từ 11 trở đi có giá là 8000 đồng. Vậy nên số tiền bạn An phải bỏ ra khi mua 25 bông hoa hồng vàng là:
10.10000 + 15.8000 = 220000 (đồng)
Nếu mua hoa hồng đỏ thì mỗi bông được giảm giá 25% khi đó giá của hoa hồng đỏ còn:
12000 – 12000. 0,25 = 9000 (đồng)
Vậy số tiền mà An phải bỏ ra khi mua 25 bông hoa hồng là:
25. 9000 = 225000 (đồng)
Ta thấy số tiền mà An bỏ ra mua hoa hồng đỏ nhiều hơn hoa hồng vàng vậy nên theo em bạn An nên mua hồng vàng để tiết kiệm chi phí hơn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 4