Câu hỏi:

25/08/2022 948

Từ vị trí A, người ta quan sát một cái cây cao mọc vuông góc với mặt đất như hình vẽ.

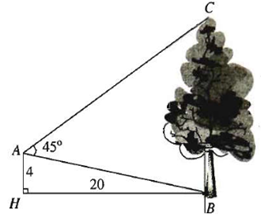
Biết vị trí quan sát cách mặt đất một khoảng AH = 4 m và khoảng cách từ chân đường vuông góc của vị trí quan sát A trên mặt đất tới gốc cây là HB = 20 m, \(\widehat {BAC} = 45^\circ \). Chiều cao của cây gần nhất với giá trị nào sau đây?

A. 17,5 m;

B. 17 m;

C. 16,5 m;

D. 16 m.

Xem lời giải

Câu hỏi trong đề: 30 câu Trắc nghiệm Toán 10 chân trời sáng tạo Bài tập ôn tập chương 4 có đáp án (Phần 2) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải

Đáp án đúng là: A

Xét ∆ABH vuông tại H có \(\tan \widehat {ABH} = \frac{{AH}}{{HB}} = \frac{4}{{20}} = \frac{1}{5}\).

Suy ra \(\widehat {ABH} \approx 11^\circ 19'\).

Ta có CB ⊥ BH (cái cây vuông góc với mặt đất)

Suy ra \(\widehat {CBH} = 90^\circ \).

Do đó \(\widehat {CBA} + \widehat {ABH} = 90^\circ \)

Vì vậy \(\widehat {CBA} = 90^\circ - \widehat {ABH} \approx 90^\circ - 11^\circ 19' = 78^\circ 41'\).

∆ABC có \(\widehat {CAB} + \widehat {CBA} + \widehat {ACB} = 180^\circ \) (định lí tổng ba góc trong một tam giác)

Suy ra \(\widehat {ACB} = 180^\circ - \left( {\widehat {CAB} + \widehat {CBA}} \right) \approx 180^\circ - \left( {45^\circ + 78^\circ 41'} \right) = 56^\circ 19'\).

∆ABH vuông tại H nên theo định lí Pythagore ta có:

AB² = AH² + BH²

= 4² + 20² = 416

Suy ra AB = \(4\sqrt {26} \) (m)

Áp dụng định lí sin cho ∆ABC, ta được \(\frac{{BC}}{{\sin \widehat {BAC}}} = \frac{{AB}}{{\sin \widehat {ACB}}}\)

Suy ra \(\frac{{BC}}{{\sin 45^\circ }} = \frac{{4\sqrt {26} }}{{\sin 56^\circ 19'}}\)

Do đó \(BC = \frac{{4\sqrt {26} .\sin 45^\circ }}{{\sin 56^\circ 19'}} \approx 17,33\) (m).

Giá trị này gần với 17,5 (m)

Vậy ta chọn phương án A.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho ∆ABC và các khẳng định sau:

(I) b² – c² = a(b.cosC – c.cosB);

(II) (b + c)sinA = a(sinB + sinC);

(III) h_a = 2R.sinB.sinC;

(IV) S = R.r.(sinA + sinB + sin C);

Số khẳng định đúng là:

A. 1;

B. 2;

C. 3;

D. 4.

Lời giải

Hướng dẫn giải

Đáp án đúng là: D

⦁ Ta xét khẳng định (I):

Áp dụng định lí côsin cho ∆ABC ta có:

b² – c² = c² + a² – 2ca.cosB – (a² + b² – 2ab.cosC)

= c² + a² – 2ca.cosB – a² – b² + 2ab.cosC

= c² – b² + 2a(b.cosC – c.cosB)

Þ b² – c² = c² – b² + 2a(b.cosC – c.cosB)

Þ 2(b² – c²) = 2a(b.cosC – c.cosB)

Þ b² – c² = a(b.cosC – c.cosB).

Do đó khẳng định (I) đúng.

⦁ Ta xét khẳng định (II):

Áp dụng hệ quả định lí sin cho ∆ABC ta có:

(b + c)sinA = \[\left( {2R.\sin B + 2R.\sin C} \right).\frac{a}{{2R}}\]

\[ = \left( {\sin B + \sin C} \right).\frac{{2R.a}}{{2R}}\]

= a(sinB + sinC).

Vì vậy khẳng định (II) đúng.

⦁ Ta xét khẳng định (III):

Áp dụng hệ quả định lí sin cho ∆ABC ta có:

2R.sinB.sinC = \(2R.\frac{b}{{2R}}.\frac{c}{{2R}}\)

\( = \frac{{bc}}{{2R}} = \frac{{abc}}{{4R}}.\frac{2}{a}\)

\( = \frac{{2S}}{a} = {h_a}\).

Vì vậy khẳng định (III) đúng.

⦁ Ta xét khẳng định (IV):

Áp dụng hệ quả định lí sin cho ∆ABC ta có:

R.r.(sinA + sinB + sin C) = \(R.r.\left( {\frac{a}{{2R}} + \frac{b}{{2R}} + \frac{c}{{2R}}} \right)\)

\[ = R.r.\frac{1}{R}\left( {\frac{a}{2} + \frac{b}{2} + \frac{c}{2}} \right)\]

\[ = r.\frac{{a + b + c}}{2} = r.p = S\].

Vì vậy khẳng định (IV) đúng.

Vậy có 4 khẳng định đúng, ta chọn phương án D.

Câu 2

Giả sử CD = h là chiều cao của tháp, trong đó C là chân tháp.

Một người đứng tại vị trí A (\(\widehat {CAD} = 63^\circ ),\) không sang được bờ bên kia để đo chiều cao h của tháp nên chọn thêm một điểm B (ba điểm A, B, C thẳng hàng) cách A một khoảng 24 m và \[\widehat {CBD} = 48^\circ \] để tính toán được chiều cao của tháp. Chiều cao h của tháp gần nhất với:

A. 18 m;

B. 18,5 m;

C. 60 m;

D. 60,5 m.

Lời giải

Hướng dẫn giải

Đáp án đúng là: D

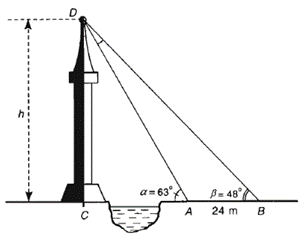
Ta có \(\widehat {CAD} + \widehat {BAD} = 180^\circ \) (hai góc kề bù).

\( \Rightarrow \widehat {BAD} = 180^\circ - \widehat {CAD} = 180^\circ - 63^\circ = 117^\circ \).

∆ABD có: \(\widehat {BAD} + \widehat {ADB} + \widehat {ABD} = 180^\circ \) (định lí tổng ba góc trong một tam giác)

\( \Rightarrow \widehat {ADB} = 180^\circ - \left( {\widehat {BAD} + \widehat {ABD}} \right) = 180^\circ - \left( {117^\circ + 48^\circ } \right) = 15^\circ \).

Áp dụng định lí sin cho ∆ABD, ta được \(\frac{{BD}}{{\sin \widehat {BAD}}} = \frac{{AB}}{{\sin \widehat {ADB}}}\)

Suy ra \(\frac{{BD}}{{\sin 117^\circ }} = \frac{{24}}{{\sin 15^\circ }}\)

Do đó \(BD = \frac{{24.\sin 117^\circ }}{{\sin 15^\circ }} \approx 82,6\) (m)

∆BCD vuông tại C: \(\sin \widehat {CBD} = \frac{{CD}}{{BD}}\).

Suy ra \(h = CD = BD.\sin \widehat {CBD} \approx 82,6.\sin 48^\circ = 61,4\) (m)

Giá trị này gần với 60,5 m.

Vậy ta chọn phương án D.

Câu 3