Câu hỏi:

11/07/2024 4,369

Cho một điểm M nằm bên ngoài đường tròn $(O; 6 c m) .$ Kẻ hai tiếp tuyến $M N, M P$ (N, P là hai tiếp điểm) của đường tròn (O). Vẽ cát tuyến MAB của đường tròn (O) sao cho đoạn thẳng $A B = 6 c m,$ với A, B thuộc đường tròn (O), A nằm giữa M và B

a, Chứng minh tứ giác OPMN nội tiếp đường tròn

Câu hỏi trong đề: Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1) !!

Sách mới 2k7: Bộ 20 đề minh họa Toán, Lí, Hóa, Văn, Sử, Địa…. form chuẩn 2025 của Bộ giáo dục (chỉ từ 49k/cuốn).

Đề toán-lý-hóa Đề văn-sử-địa Tiếng anh & các môn khác

Quảng cáo

Trả lời:

Giải bởi Vietjack

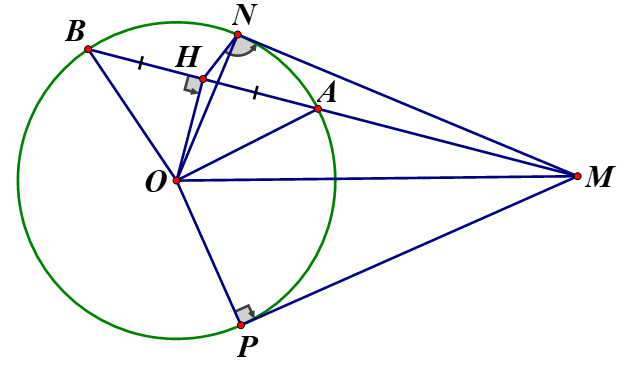
Cho một điểm M nằm bên ngoài đường tròn( O;6cm ) Kẻ hai tiếp tuyến MN, MP (ảnh 1)

a) Vì $M N, M P$ là hai tiếp tuyến $\Rightarrow \hat{N} = \hat{P} = 90^{0} \Rightarrow \hat{O N M} + \hat{O P M} = 90^{0} + 90^{0} = 180^{0}$ $\Rightarrow O N M P$ là tứ giác nội tiếp

Nhà sách VIETJACK:

Xem thêm kho sách »

Combo - Sổ tay kiên thức trọng tâm Toán, Lí, Hóa dành cho 2k7 VietJack

₫29.000 (Đã bán 152)

Sách - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 cho 2k7 VietJack

₫140.000 ₫300.000 (Đã bán 1,2k)

Sách Combo - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) - 2025 cho 2k7 VietJack

₫140.000 ₫300.000 (Đã bán 1,6k)

Sách - Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 cho 2k7 VietJack

₫140.000 ₫300.000 (Đã bán 2,7k)

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

c, Tính diện tích hình viên phân giới hạn bởi cung nhỏ AB và dây AB của đường tròn tâm (O)

Xem đáp án » 11/07/2024 9,509

Câu 2:

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

Một mảnh vườn hình chữ nhật có diện tích bằng $1200 m^{2} .$ Tính chiều dài và chiều rộng của mảnh vườn hình chữ nhật đó, biết rằng chiều dài hơn chiều rộng 10m

Xem đáp án » 11/07/2024 3,020

Câu 3:

Rút gọn các biểu thức sau:

$a) A = \sqrt{45} + \sqrt{20} - \sqrt{5}$

Xem đáp án » 11/07/2024 2,793

Câu 4:

Rút gọn các biểu thức sau:

b, $B = \frac{x + \sqrt{x}}{\sqrt{x}} + \frac{x - 4}{\sqrt{x} + 2}$ với > 0

Xem đáp án » 11/07/2024 2,751

Câu 5:

Giải phương trình và hệ phương trình:

$b) \{\begin{cases} x + 3 y = 4 \\ 2 x + 5 y = 7 \end{cases}$

Xem đáp án » 11/07/2024 2,392

Câu 6:

b, Gọi H là trung điểm của đoạn thẳng AB So sánh $\hat{M O N}$ và $\hat{M H N}$

Xem đáp án » 11/07/2024 1,685

Xem thêm các câu hỏi khác »

Nhà sách VIETJACK:

Bình luận

c, Tính diện tích hình viên phân giới hạn bởi cung nhỏ AB và dây AB của đường tròn tâm (O)

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

Một mảnh vườn hình chữ nhật có diện tích bằng $1200 m^{2} .$ Tính chiều dài và chiều rộng của mảnh vườn hình chữ nhật đó, biết rằng chiều dài hơn chiều rộng 10m

Rút gọn các biểu thức sau:

$a) A = \sqrt{45} + \sqrt{20} - \sqrt{5}$

Rút gọn các biểu thức sau:

b, $B = \frac{x + \sqrt{x}}{\sqrt{x}} + \frac{x - 4}{\sqrt{x} + 2}$ với > 0

Giải phương trình và hệ phương trình:

$b) \{\begin{cases} x + 3 y = 4 \\ 2 x + 5 y = 7 \end{cases}$

b, Gọi H là trung điểm của đoạn thẳng AB So sánh $\hat{M O N}$ và $\hat{M H N}$

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

Nhà sách VIETJACK:

Bình luận

c, Tính diện tích hình viên phân giới hạn bởi cung nhỏ AB và dây AB của đường tròn tâm (O)

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình Một mảnh vườn hình chữ nhật có diện tích bằng 1200m2. Tính chiều dài và chiều rộng của mảnh vườn hình chữ nhật đó, biết rằng chiều dài hơn chiều rộng 10m

Rút gọn các biểu thức sau: a)A=45+20−5

Rút gọn các biểu thức sau: b, B=x+xx+x−4x+2 với > 0

Giải phương trình và hệ phương trình: b)x+3y=42x+5y=7

b, Gọi H là trung điểm của đoạn thẳng AB So sánh MON^ và MHN^

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

Một mảnh vườn hình chữ nhật có diện tích bằng $1200 m^{2} .$ Tính chiều dài và chiều rộng của mảnh vườn hình chữ nhật đó, biết rằng chiều dài hơn chiều rộng 10m

Rút gọn các biểu thức sau:

$a) A = \sqrt{45} + \sqrt{20} - \sqrt{5}$

Rút gọn các biểu thức sau:

b, $B = \frac{x + \sqrt{x}}{\sqrt{x}} + \frac{x - 4}{\sqrt{x} + 2}$ với > 0

Giải phương trình và hệ phương trình:

$b) \{\begin{cases} x + 3 y = 4 \\ 2 x + 5 y = 7 \end{cases}$

b, Gọi H là trung điểm của đoạn thẳng AB So sánh $\hat{M O N}$ và $\hat{M H N}$