Câu hỏi:

13/07/2024 6,885

Cho tam giác ABC (AB<AC) nội tiếp đường tròn (O). Hai đường cao BD và CE của tam giác ABC cắt nhau tại H.Đường thẳng AH cắt BC và (O) lần lượt tại F và K $(K \neq A) .$ Gọi là hình chiếu của D lên AB.

a, Chứng minh rằng tứ giác nội tiếp BEDC và $B D^{2} = B L . B A$

Xem lời giải

Câu hỏi trong đề: Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

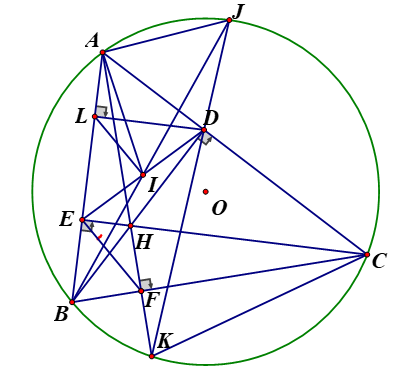
Cho tam giác ABC (AB<AC) nội tiếp đường tròn (O). Hai đường cao BD và CE của tam giác ABC (ảnh 1)

a, $\hat{B E C} = \hat{B D C} = 90^{0}$ (BD, CE là hai đường cao của tam giác ABC)

$\to$ tứ giác BEDC nội tiếp (2 đỉnh liên tiếp cùng nhìn BC)

Tam giác BDA vuông tại D có DL là đường cao nên $B D^{2} = B L . B A$

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Bạn Dũng trung bình tiêu thụ 15 ca-lo cho mỗi phút bơi và 10ca -lo ho mỗi phút chạy bộ. Hôm nay, Dũng mất1,5 giờ cho cả hai hoạt động trên và tiêu thụ hết 1200calo. Hỏi hôm nay, bạn Dũng mất bao nhiêu thời gian cho mỗi hoạt động

Xem đáp án

Lời giải

Gọi x,y (phút) lần lượt là thời gian mà Dũng đi bơi và chạy bộ

Dũng mất 1,5giờ cho cả hai hoạt động trên nên $x + y = 90$

Tiêu thụ hết 1200 ca-lo nên $15 x + 10 y = 1200$

Ta có hệ phương trình: $\{\begin{cases} x + y = 90 \\ 15 x + 10 y = 1200 \end{cases} \Leftrightarrow \{\begin{cases} x = 60 (t m) \\ y = 30 (t m) \end{cases}$

Vậy Dũng đi bơi mất 60 phút, và chạy bộ mất 30 phút

Câu 2

Cho phương trình : $2 x^{2} - 3 x - 1 = 0$ có hai nghiệm là $x_{1}, x_{2}$

Không giải phương trình, hãy tính giá trị của biểu thức : $A = \frac{x_{1} - 1}{x_{2} + 1} + \frac{x_{2} - 1}{x_{1} + 1}$

Xem đáp án

Lời giải

Tổng $x_{1} + x_{2} = \frac{3}{2}; x_{1} x_{2} = - \frac{1}{2}$

$A = \frac{x_{1}^{2} + x_{2}^{2} - 2}{x_{1} x_{2} + x_{1} + x_{2} + 1} = \frac{{(x_{1} + x_{2})}^{2} - 2 x_{1} x_{2} - 2}{x_{1} x_{2} + (x_{1} + x_{2}) + 1} = \frac{5}{8}$

Câu 3

Một nhóm gồm 31 bạn học sinh tổ chức một chuyến đi du lịch (chi phí chuyến đi được chia đều cho mỗi bạn tham gia). Sau khi đã hợp đồng xong, vào giờ chót có 3 bạn bận việt đột xuất không đi được nên họ không đóng tiền. Cả nhóm thống nhất mỗi bạn còn lại sẽ đóng thêm 18000 đồng so với dự kiến ban đầu để bù lại cho 3 bạn không tham gia. Hỏi tổng chi phí chuyến đi là bao nhiêu

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cuối năm học, các bạn lớp 9A chia làm hai nhóm, mỗi nhóm chọn một khu vườn sinh thái ở Bắc bán cầu để tham quan. Khi mở hệ thống định vị GPS, họ phát hiện một sự trùng hợp khá thú vị là hai vị trí mà hai nhóm chọn đều nằm cùng trên một kinh tuyến và lần lượt ở các vĩ tuyến

a, Tính khoảng cách (làm tròn đến hàng trăm) giữa hai vị trí đó, biết rằng kinh tuyến là một cung tròn nối liền hai cực của trái đất và có độ dài khoảng $20000 k m$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Quy tắc sau đây cho ta biết được ngày n , tháng năm 2019 là ngày thứ mấy trong tuần

Đều tiên, ta tính giá trị của biểu thức $T = n + H,$ ở đây được xác định bởi bảng sau:

Tháng t
8

2;3;11

6

9;12

4;7

1;10

5

-3

-2

- 1

0

1

2

3

Sau đó, lấy T chia cho 7 ta được số dư $r (0 \leq r \leq 6)$

Nếu $r = 0$ thì ngày đó là ngày thứ Bảy

Nếu $r = 1$ thì ngày đó là ngày Chủ Nhật

Nếu $r = 2$ thì ngày đó là ngày thứ Hai

Nếu $r = 3$ thì ngày đó là ngày thứ Ba

…….

Nếu $r = 6$ thì ngày đó là ngày thứ Sáu

Ví dụ: Ngày $31 / 12 / 2019$ có $n = 31, t = 12; H = 0 \Rightarrow T = 31 + 0 = 31;$ số chia cho 7 có số dư là 3, nên ngày đó là ngày thứ Ba.

a, Em hãy sử dụng quy tắc trên để xác định các ngày $02 / 09 / 2019$ và $20 / 11 / 2019$ là thứ mấy ?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

b,Bạn Hằng tổ chức sinh nhật của mình trong tháng $10 / 2019.$ Hỏi sinh nhật của bạn Hằng là ngày mấy? Biết rằng ngày sinh nhật của Hằng là một bội số của 3 và là thứ Hai

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bạn Dũng trung bình tiêu thụ 15 ca-lo cho mỗi phút bơi và 10ca -lo ho mỗi phút chạy bộ. Hôm nay, Dũng mất1,5 giờ cho cả hai hoạt động trên và tiêu thụ hết 1200calo. Hỏi hôm nay, bạn Dũng mất bao nhiêu thời gian cho mỗi hoạt động

Cho phương trình :2x2−3x−1=0 có hai nghiệm là x1,x2 Không giải phương trình, hãy tính giá trị của biểu thức : A=x1−1x2+1+x2−1x1+1

b,Bạn Hằng tổ chức sinh nhật của mình trong tháng 10/2019. Hỏi sinh nhật của bạn Hằng là ngày mấy? Biết rằng ngày sinh nhật của Hằng là một bội số của 3 và là thứ Hai

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho phương trình : $2 x^{2} - 3 x - 1 = 0$ có hai nghiệm là $x_{1}, x_{2}$

Không giải phương trình, hãy tính giá trị của biểu thức : $A = \frac{x_{1} - 1}{x_{2} + 1} + \frac{x_{2} - 1}{x_{1} + 1}$

b,Bạn Hằng tổ chức sinh nhật của mình trong tháng $10 / 2019.$ Hỏi sinh nhật của bạn Hằng là ngày mấy? Biết rằng ngày sinh nhật của Hằng là một bội số của 3 và là thứ Hai