Câu hỏi:
24/10/2022 675
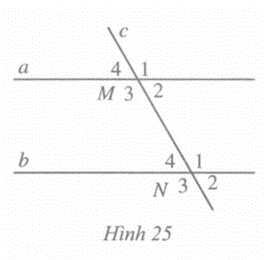
Quan sát Hình 25, biết a // b.
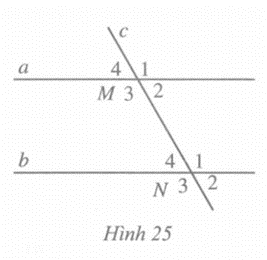
So sánh \(\widehat {{M_1}}\) và \(\widehat {{N_3}}\); \(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) (mỗi cặp \(\widehat {{M_1}}\) và \(\widehat {{N_3}}\), \(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) gọi là một cặp góc so le ngoài).
Quan sát Hình 25, biết a // b.
So sánh \(\widehat {{M_1}}\) và \(\widehat {{N_3}}\); \(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) (mỗi cặp \(\widehat {{M_1}}\) và \(\widehat {{N_3}}\), \(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) gọi là một cặp góc so le ngoài).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Do a // b nên \(\widehat {{M_1}} = \widehat {{N_1}}\) (hai góc đồng vị).
Mặt khác \(\widehat {{N_1}} = \widehat {{N_3}}\) (hai góc đối đỉnh). Suy ra: \(\widehat {{M_1}}\)= \(\widehat {{N_3}}\).
Do a // b nên \(\widehat {{M_4}}\) = \(\widehat {{N_4}}\) (hai góc đồng vị).
Mặt khác \(\widehat {{N_4}}\) = \(\widehat {{N_2}}\) (hai góc đối đỉnh). Suy ra: \(\widehat {{M_4}}\)= \(\widehat {{N_2}}\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
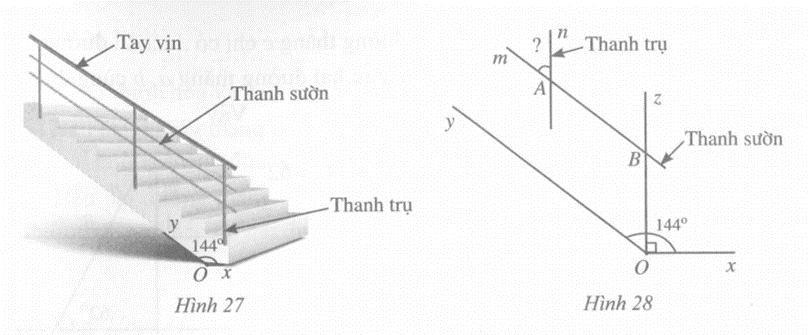
Ta có góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can bằng góc mAn.
Do An // Bz nên \(\widehat {mAn} = \widehat {ABz}\) (hai góc đồng vị). Do AB // Oy nên \(\widehat {ABz} = \widehat {BOy}\) (hai góc đồng vị). Từ đó, ta có: \(\widehat {mAn} = \widehat {BOy}\).
Ta có \(\widehat {BOy} + \widehat {BOx} = 144^\circ \) (hai góc kề nhau) và \(\widehat {BOx} = 90^\circ \) suy ra \(\widehat {BOy} = 54^\circ \) hay \(\widehat {mAn} = 54^\circ \).
Vậy góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can bằng 54°.
Lời giải
Ta có: \(\widehat {{M_2}} + \widehat {{M_1}}\) = 180° (hai góc kề bù)
Lại có a // b nên \(\widehat {{M_1}} = \widehat {{N_1}}\) (hai góc đồng vị). Suy ra: \(\widehat {{M_2}} + \widehat {{N_1}}\)= 180°.
Tương tự, ta có: \(\widehat {{M_3}} + \widehat {{M_4}} = 180^\circ \) (hai góc kề bù)
Lại có a // b nên \(\widehat {{M_4}} = \widehat {{N_4}}\) (hai góc đồng vị). Suy ra: \(\widehat {{M_3}} + \widehat {{N_4}}\)= 180°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2
-
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án