Câu hỏi:
24/10/2022 1,307
Để đảm bảo an toàn khi đi lại trên cầu thang của ngôi nhà, người ta phải làm lan can. Phía trên của lan can có tay vịn làm chỗ dựa để khi lên xuống cầu thang được thuận tiện. Phía dưới tay vịn là các thanh trụ song song với nhau và các thanh sườn song song với nhau. Để đảm bảo chắc chắn thì các thanh trụ của lan can được gắn vuông góc cố định xuống bậc cầu thang.
Trong Hình 27, góc xOy bằng 144°. Hỏi góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can là bao nhiêu độ ? (Xem hướng dẫn ở Hình 28).
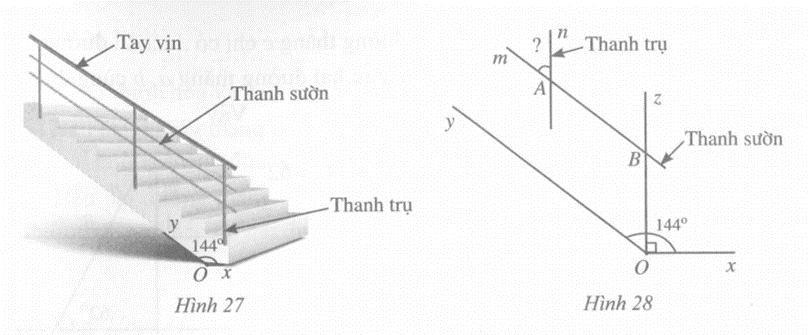
Để đảm bảo an toàn khi đi lại trên cầu thang của ngôi nhà, người ta phải làm lan can. Phía trên của lan can có tay vịn làm chỗ dựa để khi lên xuống cầu thang được thuận tiện. Phía dưới tay vịn là các thanh trụ song song với nhau và các thanh sườn song song với nhau. Để đảm bảo chắc chắn thì các thanh trụ của lan can được gắn vuông góc cố định xuống bậc cầu thang.
Trong Hình 27, góc xOy bằng 144°. Hỏi góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can là bao nhiêu độ ? (Xem hướng dẫn ở Hình 28).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can bằng góc mAn.
Do An // Bz nên \(\widehat {mAn} = \widehat {ABz}\) (hai góc đồng vị). Do AB // Oy nên \(\widehat {ABz} = \widehat {BOy}\) (hai góc đồng vị). Từ đó, ta có: \(\widehat {mAn} = \widehat {BOy}\).
Ta có \(\widehat {BOy} + \widehat {BOx} = 144^\circ \) (hai góc kề nhau) và \(\widehat {BOx} = 90^\circ \) suy ra \(\widehat {BOy} = 54^\circ \) hay \(\widehat {mAn} = 54^\circ \).
Vậy góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can bằng 54°.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
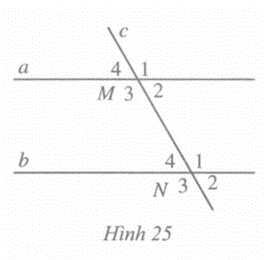
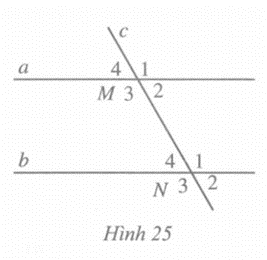
Ta có: \(\widehat {{M_2}} + \widehat {{M_1}}\) = 180° (hai góc kề bù)
Lại có a // b nên \(\widehat {{M_1}} = \widehat {{N_1}}\) (hai góc đồng vị). Suy ra: \(\widehat {{M_2}} + \widehat {{N_1}}\)= 180°.
Tương tự, ta có: \(\widehat {{M_3}} + \widehat {{M_4}} = 180^\circ \) (hai góc kề bù)
Lại có a // b nên \(\widehat {{M_4}} = \widehat {{N_4}}\) (hai góc đồng vị). Suy ra: \(\widehat {{M_3}} + \widehat {{N_4}}\)= 180°.
Lời giải
Theo tiên đề Euclid thì qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Như thế, qua điểm M không thuộc đường thẳng c chỉ có một đường thẳng song song với đường thẳng c, tức là nếu hai đường thẳng a, b cùng đi qua M và cùng song song với c thì a và b trùng nhau. Vậy bạn Hải nói đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2
-
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án